Question

设定义域为R的函数f（x）={

|lgx|，x＞0 -x2-2x，x≤0

，若关于x的函数y=2f²（x）+mf（x）+1有8个不同的零点，则实数m的取值范围是

 

．

Answer 1

考点：函数零点的判定定理,分段函数的应用

专题：计算题,函数的性质及应用

分析：先将函数进行换元，转化为一元二次函数问题．结合函数f（x）的图象，从而确定b的取值范围．

解答： 解：令t=f（x），则原函数等价为y=2t²+mt+1．做出函数f（x）的图象如图，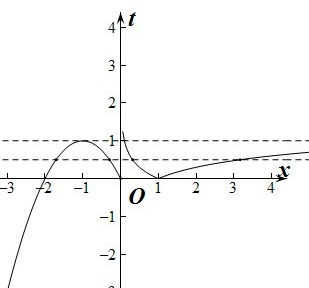
图象可知当由0＜t＜1时，函数t=f（x）有四个交点．
要使关于x的函数y=2f²（x）+mf（x）+1有8个不同的零点，则函数y=2t²+mt+1有两个根t₁，t₂，
且0＜t₁＜1，0＜t₂＜1．
令g（t）=2t²+mt+1，则由根的分布可得

m2-8＞0 g(0)＞0 g(1)=m+3＞0 0＜- m 4 ＜1

，
故实数m的取值范围是-3＜m＜-2

2

．
故答案为：-3＜m＜-2

2

点评：本题考查复合函数零点的个数问题，以及二次函数根的分布，换元是解决问题的关键，属中档题．