题目内容
若M为圆x2+y2=1上的点,求M到直线3x+4y-25=0的最小距离,并求出点M的坐标.
考点:直线与圆的位置关系
专题:直线与圆
分析:圆心(0,0)到直线3x+4y-25=0的距离d=5,M点到直线3x+4y-25=0距离的最小值是5-r=5-1=4,M到直线3x+4y-25=0的距离最小时,过圆心和M点的直线与直线3x+4y-25=0垂直,由此能求出点M的坐标.
解答:
解:∵圆心(0,0)到直线3x+4y-25=0的距离d=
=5,
∴如图,当M与A重合时,
M点到直线3x+4y-25=0距离的最小值是:
AC=5-r=5-1=4,
∵M到直线3x+4y-25=0的距离最小时,
BC⊥直线3x+4y-25=0,
∴kBC=
,∴直线BC:y=
x,
联立
,得A(
,
),C(-
,-
),
∴M到直线3x+4y-25=0的距离最小时,
点M的坐标为M(
,
).
| |0+0-25| | ||
|

∴如图,当M与A重合时,
M点到直线3x+4y-25=0距离的最小值是:
AC=5-r=5-1=4,
∵M到直线3x+4y-25=0的距离最小时,
BC⊥直线3x+4y-25=0,
∴kBC=
| 4 |
| 3 |
| 4 |
| 3 |
联立
|
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∴M到直线3x+4y-25=0的距离最小时,
点M的坐标为M(
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题考查M到直线3x+4y-25=0的最小距离的求法,考查点的坐标的求法,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
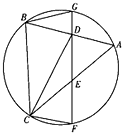 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD. 如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.
如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明. 某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,成绩如下表:
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,成绩如下表: