题目内容
满足M⊆{0，1，2}且M⊆{0，2，4}的集合M有 ．
考点：子集与真子集
专题：集合
分析：由M⊆{0，1，2}且M⊆{0，2，4}可得：M⊆{0，1，2}∩{0，2，4}={0，2}，进而得到答案．
解答：
解：M⊆{0，1，2}且M⊆{0，2，4}
故M⊆{0，1，2}∩{0，2，4}={0，2}，
由于{0，2}有两个元素，
故满足条件的M有22=4个，
故答案为：4
故M⊆{0，1，2}∩{0，2，4}={0，2}，
由于{0，2}有两个元素，
故满足条件的M有22=4个，
故答案为：4
点评：本题考查了子集与真子集，是基础的概念题．
练习册系列答案
相关题目
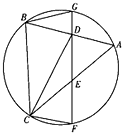如图，D，E分别是△ABC的边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，BG=BD．
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试，成绩如下表：