题目内容
给出下列说法:
①存在实数α,使sinα+cosα=
;
②函数y=sin(
π+x)是奇函数;
③x=
是函数y=sin(2x+
π)的一条对称轴方程;
④若tanα=-
,则
=
.
其中正确说法的序号是 .
①存在实数α,使sinα+cosα=
| 3 |
| 2 |
②函数y=sin(
| 3 |
| 2 |
③x=
| π |
| 8 |
| 5 |
| 4 |
④若tanα=-
| 1 |
| 3 |
| 1 |
| cos2α |
| 10 |
| 9 |
其中正确说法的序号是
考点:命题的真假判断与应用
专题:三角函数的求值,三角函数的图像与性质
分析:利用两角和与差的三角函数以及三角函数的值域判断①的正误;
利用三角函数的奇偶性判断②的正误;
利用三角函数的对称性判断③的正误;
利用同角三角函数的基本关系式求解判断④的正误.
利用三角函数的奇偶性判断②的正误;
利用三角函数的对称性判断③的正误;
利用同角三角函数的基本关系式求解判断④的正误.
解答:
解:对于①,sinα+cosα=
sin(α+45°)≤
<
,∴①不正确;
对于②,函数y=sin(
π+x)=-cosx是偶函数,判断为奇函数不正确;
对于③,x=
时,函数y=sin(2×
+
π)=-1,函数取得最值,所以x=
是函数的一条对称轴方程③正确;
对于④,tanα=-
,则
=
=tan2α+1=
.所以④正确;
故答案为:③④.
| 2 |
| 2 |
| 3 |
| 2 |
对于②,函数y=sin(
| 3 |
| 2 |
对于③,x=
| π |
| 8 |
| π |
| 8 |
| 5 |
| 4 |
| π |
| 8 |
对于④,tanα=-
| 1 |
| 3 |
| 1 |
| cos2α |
| sin2α+cos2α |
| cos2α |
| 10 |
| 9 |
故答案为:③④.
点评:本题考查命题的真假的判断,三角函数的基本性质以及三角函数的值域的求法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
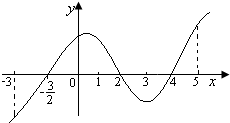 如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论:
如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论: