题目内容
17.对于曲线C所在平面内的点O,若存在以O为顶点的角θ,使得θ≥∠AOB对于曲线C上的任意两个不同点A、B恒成立,则称θ为曲线C相对于O的“界角”,并称最小的“界角”为曲线C相对于O的“确界角”,已知曲线M:y=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2}},x≤0}\\{1+x{e}^{x-1},x>0}\end{array}\right.$,(其中e为自然对数的底数),O为坐标原点,则曲线M相对于O的“确界角”为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
分析 画出函数f(x)的图象,过点O作出两条直线与曲线无限接近,当x≤0时,曲线y=$\sqrt{1+9{x}^{2}}$与直线y=k1x无限接近,考虑渐近线,求出k1=-3;当x>0时,设出切点,求出切线的斜率,列出方程,求出切点(1,2),即得k2=2,再由两直线的夹角公式即可得到所求的“确界角”.
解答 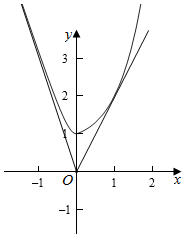 解:画出函数f(x)的图象,过点O作出两条直线与曲线无限接近,设它们的方程分别为y=k1x,y=k2x,
解:画出函数f(x)的图象,过点O作出两条直线与曲线无限接近,设它们的方程分别为y=k1x,y=k2x,
当x≤0时,曲线y=$\sqrt{1+9{x}^{2}}$与直线y=k1x无限接近,即为双曲线的渐近线,故k1=-3;
当x>0时,y′=ex-1+xex-1,设切点为(m,n),则n=k2m,
n=mem-1+1,k2=em-1+mem-1,即有m2em-1=1,
由x2ex-1(x>0)为增函数,且x=1成立,故m=1,k2=2,
由两直线的夹角公式得,tanθ=|$\frac{2-(-3)}{1+2×(-3)}$|=1,
故曲线C相对于点O的“确界角”为$\frac{π}{4}$.
故选:B.
点评 本题考查新定义“确界角”及应用,考查导数的应用:求切线,双曲线的性质:渐近线,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.在下列函数中,是偶函数,且在(0,+∞)内单调递增的是( )
| A. | y=2|x| | B. | $y=\frac{1}{x^2}$ | C. | y=|lgx| | D. | y=cosx |
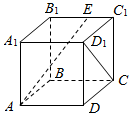 如图,在正方体ABCD-A1B1C1D1中,E是线段B1C1上的动点,则异面直线AE与直线D1C所成的角为90°.
如图,在正方体ABCD-A1B1C1D1中,E是线段B1C1上的动点,则异面直线AE与直线D1C所成的角为90°.