题目内容
7．函数y=x2+ln|x|的图象大致为（ ）| A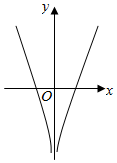． |  | B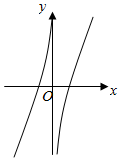． |  | C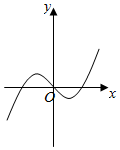． |  | D． |  |
分析 先求出函数为偶函数，再根据函数值的变化趋势或函数的单调性即可判断．
解答 解：∵f（-x）=x2+ln|x|=f（x），
∴y=f（x）为偶函数，
∴y=f（x）的图象关于y轴对称，故排除B，C，
当x→0时，y→-∞，故排除D，
或者根据，当x＞0时，y=x2+lnx为增函数，故排除D，
故选：A
点评 本题考查了函数图象的识别，关键是掌握函数的奇偶性和函数的单调性和函数值的变化趋势，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
18．已知幂函数f（x）=xα（α为常数）的图象过点$P（{2，\frac{1}{2}}）$，则f（x）的单调递减区间是（ ）
| A． | （-∞，0） | B． | （-∞，+∞） | C． | （-∞，0）∪（0，+∞） | D． | （-∞，0）与（0，+∞） |
15．
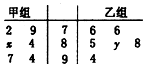如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩（单位：分），已知甲组数据的众数为84，乙组数据的平均数即为甲组数据的中位数，则x，y的值分别为（ ）
如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩（单位：分），已知甲组数据的众数为84，乙组数据的平均数即为甲组数据的中位数，则x，y的值分别为（ ）| A． | 4，5 | B． | 5，4 | C． | 4，4 | D． | 5，5 |
12．已知A（-3，0），B（0，4），点P为直线y=x上一点，过A，B，P三点的圆记作圆C，则“点P为原点”是“圆C的半径取得最小值”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |