题目内容
17.将正弦曲线y=sinx上所有的点向右平移$\frac{2}{3}$π个单位长度,再将图象上所有点的横坐标变为原来的$\frac{1}{3}$倍(纵坐标不变),则所得到的图象的函数解析式y=$sin(3x-\frac{2π}{3})$.分析 先根据左加右减进行左右平移,然后根据横坐标伸长到原来的$\frac{1}{3}$倍时,x的系数变为原来的3倍进行横向变换.从而可得函数解析式.
解答 解:由题意,将函数y=sinx的图象上所有的点向右平行移动$\frac{2}{3}$π个单位长度,
利用左加右减,可所函数图象的解析式为y=sin(x-$\frac{2}{3}$π),
再把所得各点的横坐标伸长到原来的$\frac{1}{3}$倍(纵坐标不变),利用x的系数变为原来的3倍进行横向变换,
可得图象的函数解析式是$y=sin(3x-\frac{2π}{3})$.
故答案为:$sin(3x-\frac{2π}{3})$.
点评 本题的考点是利用图象变换得函数解析式,主要考查三角函数的平移变换,周期变换.关键是利用平移的原则是左加右减、上加下减.

练习册系列答案
相关题目
7.函数y=x2+ln|x|的图象大致为( )
| A. | 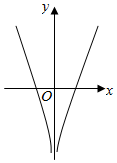 | B. | 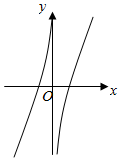 | C. | 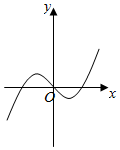 | D. |  |
9.半径为R的半圆卷成底面最大的圆锥,所得圆锥的高为( )
| A. | $\sqrt{3}R$ | B. | $\frac{{\sqrt{3}}}{2}R$ | C. | $\sqrt{2}R$ | D. | $\frac{{\sqrt{2}}}{2}R$ |