题目内容
15.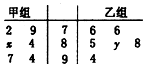 如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )
如图叶茎图记录了甲、乙两组各6名学生在一次数字测试中的成绩(单位:分),已知甲组数据的众数为84,乙组数据的平均数即为甲组数据的中位数,则x,y的值分别为( )| A. | 4,5 | B. | 5,4 | C. | 4,4 | D. | 5,5 |
分析 由茎叶图中甲组的数据,根据它们的众数,求出x的值,得出甲组数据的中位数,再求乙组数据的平均数,即得y的值.
解答 解:根据茎叶图的数据知,甲组数据是
72,79,84,(80+x),94,97,
它们的众数是84,∴x=4;
∴甲组数据的中位数是84,
∴乙组数据的平均数为84
即$\frac{1}{6}$×(76+76+85+80+y+88+94)=84,
解得y=5;
∴x、y的值分别为4、5.
故选:A.
点评 本题考查了茎叶图的应用问题,解题时应根据茎叶图的数据,求出它们的平均数与中位数,从而求出x、y的值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
5.过抛物线y2=4ax(a>0)的焦点F作斜率为-1的直线l,l与离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({b>0})$的两条渐近线的交点分别为B,C.若xB,xC,xF分别表示B,C,F的横坐标,且$x_F^2=-{x_B}•{x_C}$,则e=( )
| A. | 6 | B. | $\sqrt{6}$ | C. | 3 | D. | $\sqrt{3}$ |
3.已知x∈R,用[x]表示不超过x的最大整数,记{x}=x-[x],若a∈(0,1),且$\{a\}>\{a+\frac{1}{3}\}$,则实数a的取值范围是[$\frac{2}{3}$,+∞).
10.已知函数f(x)=ex+2(x<0)与g(x)=ln(x+a)+2的图象上存在关于y轴对称的点,则实数a的取值范围是( )
| A. | (-∞,e) | B. | (0,e) | C. | (e,+∞) | D. | (-∞,1) |
7.函数y=x2+ln|x|的图象大致为( )
| A. | 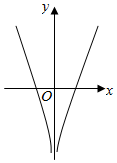 | B. | 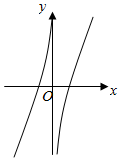 | C. | 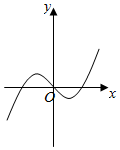 | D. |  |
4.已知三条不同的直线a,b,c,若a⊥b,则“a⊥c”是“b∥c”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
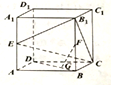 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.