题目内容
12.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则必有( )| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{b}$=0 | C. | $\overrightarrow{a}•\overrightarrow{b}$=0 | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
分析 由条件利用两个向量的加减法及其几何意义可得以$\overrightarrow{a}$、$\overrightarrow{b}$为邻边的平行四边形为矩形,可得两个向量垂直,从而得出结论.
解答 解:根据向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,可得以$\overrightarrow{a}$、$\overrightarrow{b}$为邻边的平行四边形的两条对角线的长相等,
故有该平行四边形为矩形,故有 $\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=0,
故选:C.
点评 本题主要考查两个向量的加减法及其几何意义,两个向量垂直的性质,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.函数f(x)=sin(2x-$\frac{π}{3}$),x∈[-$\frac{π}{2}$,π],则以下结论正确的是( )
| A. | 函数f(x)在[-$\frac{π}{2}$,0]上单调递减 | B. | 函数f(x)在[0,$\frac{π}{2}$]上单调递增 | ||
| C. | 函数f(x)在[$\frac{π}{2}$,$\frac{5π}{6}$]上单调递减 | D. | 函数f(x)在[$\frac{5π}{6}$,π]上单调递增 |
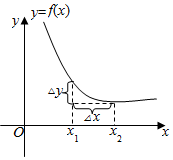 已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.
已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.