题目内容
7.求(1+2x)10的展开式中(1)求二项式系数最大的项;
(2)求系数最大的项.
分析 (1)由已知二项式可知展开式由11项,则中间一项的二项式系数最大,由此求得二项式系数最大的项;
(2)写出二项展开式的通项,由题意可得$\left\{\begin{array}{l}{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r-1}{2}^{r-1}}\\{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r+1}{2}^{r+1}}\end{array}\right.$,求得r的范围得答案.
解答 解:(1)(1+2x)10的展开式中共有11项,
中间一项的二项式系数最大,T6=${C}_{10}^{5}$25x5;
(2)(1+2x)10的展开式的通项公式为${T}_{r+1}={C}_{10}^{r}{2}^{r}{x}^{r}$,
由$\left\{\begin{array}{l}{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r-1}{2}^{r-1}}\\{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r+1}{2}^{r+1}}\end{array}\right.$,解得$\frac{19}{3}≤r≤\frac{22}{4}$,故r=7.
即系数最大的项为第8项,为${T}_{8}={C}_{10}^{8}{2}^{7}{x}^{7}$.
点评 本题考查二项式系数的性质,熟记二项展开式的通项,同时注意二项式系数与项的系数的区别,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
17.如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$的共轭复数是( )


| A. | i | B. | -i | C. | $\frac{3}{5}$i | D. | -$\frac{3}{5}$i |
2.如图所示,双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,M,N为双曲线C上两点,且kMN=0,若$\overrightarrow{{F}_{1}Q}$=$\overrightarrow{QN}$(Q在双曲线C上),且|MN|=$\frac{{|F}_{1}{F}_{2}|}{4}$,则双曲线C的渐近线方程为( )
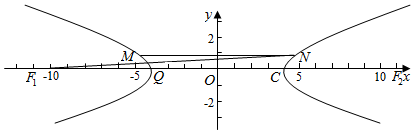
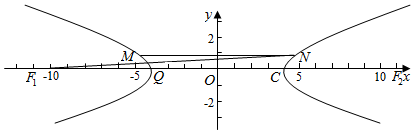
| A. | y=$±\sqrt{2}$x | B. | y=$±\sqrt{3}$x | C. | y=±2x | D. | y=$±\sqrt{5}$x |
12.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则必有( )
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{b}$=0 | C. | $\overrightarrow{a}•\overrightarrow{b}$=0 | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
16.过直线x+y=2与x-y=0的交点,且法向量为$\overrightarrow{n}$=(2,-3)的直线方程是( )
| A. | -3x+2y+1=0 | B. | 3x-2y+1=0 | C. | -2x+3y+1=0 | D. | 2x-3y+1=0 |