已知函数y=f(x)的图象如图.自变量x从x1变到x2.对应的函数y从f(x1)变到f(x2).设△x=x2-x1.确定各图的中△x.△y.$\frac{△y}{△x}$的正负．题目和参考答案——青夏教育精英家教网—

题目内容

17．

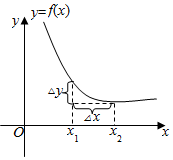已知函数y=f（x）的图象如图，自变量x从x₁变到x₂，对应的函数y从f（x₁）变到f（x₂），设△x=x₂-x₁，确定各图的中△x，△y，$\frac{△y}{△x}$的正负．

分析由图象可知函数为减函数，即可判断答案．

解答解：由图象可知函数为减函数，自变量x从x₁变到x₂，对应的函数y从f（x₁）变到f（x₂），设△x=x₂-x₁，
∴△x=x₂-x₁＞0，△y=f（x₂）-f（x₁）＜0，
∴$\frac{△y}{△x}$＜0．

点评本题考查了函数图象的识别，关键是掌握函数的单调性，以及导数的定义，属于基础题．

练习册系列答案

8．某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品需用4个A配件耗时1h，每生产一件乙产品需用4个B配件耗时2h，该厂每天最多可从配件厂获得24个A配件和16个B配件，每天生产总耗时不超过8h．若生产一件甲产品获利3万元，生产一件乙产品获利4万元，则通过恰当的生产安排，该工厂每天可获得的最大利润为（　　）

5．已知函数f（x）=2cos（2x+φ）（|φ|＜$\frac{π}{2}$）在区间（$\frac{π}{6}$，$\frac{5π}{12}$]上单调，则2sin（φ-$\frac{π}{3}$）的取值范围（-$\sqrt{3}$，-1]．

12．若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则必有（　　）

A．

$\overrightarrow{a}$=$\overrightarrow{b}$

B．

$\overrightarrow{b}$=0

C．

$\overrightarrow{a}•\overrightarrow{b}$=0

D．

|$\overrightarrow{a}$|=|$\overrightarrow{b}$|

2．已知直线l过点（0，3），且倾斜角是直线y=2x+1的倾斜角的二倍，求直线l的方程．

9．已知$\overrightarrow{a}$，$\overrightarrow{b}$为同一平面内两个不共线的向量，且$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，6），若|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$，向量$\overrightarrow{c}$=2$\overrightarrow{a}$$+\overrightarrow{b}$，则$\overrightarrow{c}$=（　　）

6．|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{a}$$•\overrightarrow{b}$=0，且$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$垂直，求实数k的值．

12．数列{a_n}中，a₁=1，a_n+1=3a_n+4，则数列{a_n}的前n项和等于（　　）

A．

$\frac{{3}^{n+1}-4n-3}{2}$

B．

$\frac{{3}^{n}-2n-1}{2}$

C．

$\frac{{3}^{n}-2n+1}{2}$

D．

3ⁿ⁺¹-2n-1

试题分类