题目内容
3.AC是圆的直径,B、D在圆上且AB=$\sqrt{3}$,AD=$\sqrt{5}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=2.分析 可连接CD,CB,从而得到CD⊥AD,BC⊥AB,便可得到$\overrightarrow{AC}$在$\overrightarrow{AD}$方向上的投影就是AD,所以$\overrightarrow{AC}$$•\overrightarrow{BD}$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=$\overrightarrow{|AC}||\overrightarrow{AD}|•COS∠CAD$-$|\overrightarrow{AC}||\overrightarrow{AB}|COS∠CAB$=AD2-AB2.
解答 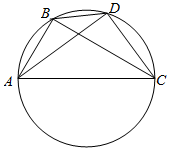 解:如图,连接CD,CB;
解:如图,连接CD,CB;
∵AC为直径;
∴CD⊥AD,BC⊥AB;
∴$\overrightarrow{AC}$$•\overrightarrow{BD}$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=$\overrightarrow{|AC}||\overrightarrow{AD}|•COS∠CAD$-$|\overrightarrow{AC}||\overrightarrow{AB}|COS∠CAB$=AD2-AB2=5-3=2;
故答案为:2.
点评 本题考查直径所对的圆周角为直角,余弦函数的定义,以及向量减法的几何意义,向量数量积的运算关键明确$\overrightarrow{AC}$在两个向量方向的投影;属于中档题.

练习册系列答案
相关题目
13.函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的最小正周期为π,将其图象向右平移$\frac{π}{3}$个单位后所得图象对应的解析式为( )
| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=-cos2x | C. | y=sin$\frac{x}{2}$ | D. | y=cos2x |
11.将向量$\overrightarrow{OA}=({1,1})$绕原点O逆时针方向旋转60°得到$\overrightarrow{OB}$,则$\overrightarrow{OB}$=( )
| A. | $({\frac{{1-\sqrt{3}}}{2},\frac{{1+\sqrt{3}}}{2}})$ | B. | $({\frac{{1+\sqrt{3}}}{2},\frac{{1-\sqrt{3}}}{2}})$ | C. | $({\frac{{-1-\sqrt{3}}}{2},\frac{{-1+\sqrt{3}}}{2}})$ | D. | $({\frac{{-1+\sqrt{3}}}{2},\frac{{-1-\sqrt{3}}}{2}})$ |
8.某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品需用4个A配件耗时1h,每生产一件乙产品需用4个B配件耗时2h,该厂每天最多可从配件厂获得24个A配件和16个B配件,每天生产总耗时不超过8h.若生产一件甲产品获利3万元,生产一件乙产品获利4万元,则通过恰当的生产安排,该工厂每天可获得的最大利润为( )
| A. | 24万元 | B. | 22万元 | C. | 18万元 | D. | 16万元 |
12.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则必有( )
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{b}$=0 | C. | $\overrightarrow{a}•\overrightarrow{b}$=0 | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
13.长郡中学早上8点开始上课,若学生小典与小方匀在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小典比小方至少早5分钟到校的概率为( )
| A. | $\frac{9}{32}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{64}$ | D. | $\frac{5}{64}$ |