题目内容
过抛物线y2=4x的焦点F的直线交该抛物线于A, B两点,O为坐标原点。
若|AF|=3,则△AOB的面积为
A. B.
B.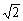 C.
C. D.2
D.2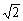
C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
过抛物线y2=4x的焦点F的直线交该抛物线于A, B两点,O为坐标原点。
若|AF|=3,则△AOB的面积为
A. B.
B.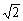 C.
C. D.2
D.2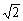
C

 阅读快车系列答案
阅读快车系列答案