题目内容
某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。
(1)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
(1)设小李四次测试合格的概率依次为:
a, a+ , a+
, a+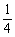 , a+
, a+ (a≤
(a≤ ), …………(2分)
), …………(2分)
则(1-a)(a+ )=
)= ,即
,即 ,
,
解得 (舍), …………(5分)
(舍), …………(5分)
所以小李第一次参加测试就合格的概率为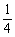 ; …………(6分)
; …………(6分)
(2)因为P(x=1)=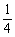 , P(x=2)=
, P(x=2)= ,P(x=3)=
,P(x=3)= ,
,
P(x=4)=1-P(x=1)-P(x=2)-P(x=3)= , …………(8分)
, …………(8分)
则x的分布列为
| x | 1 | 2 | 3 | 4 |
| P |
|
|
|
|

练习册系列答案
相关题目

 B.
B. C.
C. D.2
D.2 )的图像可由曲线y=1+cos2x向左平移
)的图像可由曲线y=1+cos2x向左平移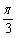 个单位得到;②函数y=sin(x+
个单位得到;②函数y=sin(x+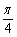 )+cos(x+
)+cos(x+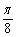 是曲线y=sin(2x+
是曲线y=sin(2x+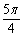 )的一条对称轴;④函数y=2sin2(x+
)的一条对称轴;④函数y=2sin2(x+ 的虚部是
的虚部是 B.
B.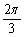 )+sin(wx-
)+sin(wx-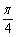 )上单调递增 B.f(x)在(0,
)上单调递增 B.f(x)在(0,  )上单调递增 D.f(x)在(0,
)上单调递增 D.f(x)在(0,  为参数),则直线L的倾斜角的余弦值为( )
为参数),则直线L的倾斜角的余弦值为( ) B.
B. C.
C. D.
D.
 是第二象限角,角
是第二象限角,角 ,且
,且 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.