题目内容
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点。
(1)求证:直线BD⊥平面OAC;
(2)求点A到平面OBD的距离。
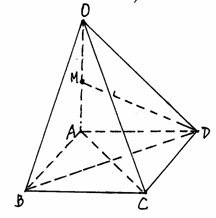
解:(1)证明:ABCD为正方形 BD⊥AC
BD⊥AC

 OA⊥平面ABCD
OA⊥平面ABCD  BD⊥平面OAC
BD⊥平面OAC
 OA⊥BD
OA⊥BD
BD 平面ABCD
平面ABCD
(2)设点A到平面OBD的距离为h
S△ABD=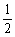 ×AB×AD=
×AB×AD=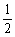 ,S△OBD=
,S△OBD=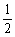 ×
× ×
× =
= 。
。
由VA-OBD=VO-ABD得 S△OBD×h=
S△OBD×h= S△ABD×OA
S△ABD×OA h=
h=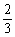
所以点A到平面OBD的距离为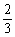

练习册系列答案
相关题目
 对任意
对任意 满足
满足 ,且当
,且当 时,
时, ,则
,则 的值为__________.
的值为__________.

 B.
B. C.
C. D.2
D.2 为参数),则直线L的倾斜角的余弦值为( )
为参数),则直线L的倾斜角的余弦值为( ) B.
B. C.
C. D.
D.