题目内容
已知函数f(x)=ex-e-x-2x.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值;
(Ⅲ)已知1.4142<
<1.4143,估计ln2的近似值(精确到0.001).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值;
(Ⅲ)已知1.4142<
| 2 |
考点:利用导数研究函数的单调性
专题:压轴题,导数的综合应用
分析:对第(Ⅰ)问,直接求导后,利用基本不等式可达到目的;
对第(Ⅱ)问,先验证g(0)=0,只需说明g(x)在[0+∞)上为增函数即可,从而问题转化为“判断g′(x)>0是否成立”的问题;
对第(Ⅲ)问,根据第(Ⅱ)问的结论,设法利用
的近似值,并寻求ln2,于是在b=2及b>2的情况下分别计算g(ln
),最后可估计ln2的近似值.
对第(Ⅱ)问,先验证g(0)=0,只需说明g(x)在[0+∞)上为增函数即可,从而问题转化为“判断g′(x)>0是否成立”的问题;
对第(Ⅲ)问,根据第(Ⅱ)问的结论,设法利用
| 2 |
| 2 |
解答:
解:(Ⅰ)由f(x)得f′(x)=ex+e-x-2≥2
-2=0,
即f′(x)≥0,当且仅当ex=e-x即x=0时,f′(x)=0,
∴函数f(x)在R上为增函数.
(Ⅱ)g(x)=f(2x)-4bf(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,
则g′(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]
=2[(ex+e-x)2-2b(ex+e-x)+(4b-4)]
=2(ex+e-x-2)(ex+e-x+2-2b).
①∵ex+e-x≥2,ex+e-x+2≥4,
∴当2b≤4,即b≤2时,g′(x)≥0,当且仅当x=0时取等号,
从而g(x)在R上为增函数,而g(0)=0,
∴x>0时,g(x)>0,符合题意.
②当b>2时,若x满足2<ex+e-x<2b-2即
,得0<x<ln(b-1+
),此时,g′(x)<0,
又由g(0)=0知,当0<x≤ln(b-1+
)时,g(x)<0,不符合题意.
综合①、②知,b≤2,得b的最大值为2.
(Ⅲ)∵1.4142<
<1.4143,根据(Ⅱ)中g(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,
为了凑配ln2,并利用
的近似值,故将ln
即
ln2代入g(x)的解析式中,
得g(ln
)=
-2
b+2(2b-1)ln2.
当b=2时,由g(x)>0,得g(ln
)=
-4
+6ln2>0,
从而ln2>
>
=0.6928;
令ln(b-1+
)=ln
,得b=
+1>2,当0<x≤ln(b-1+
)时,
由g(x)<0,得g(ln
)=-
-2
+(3
+2)ln2<0,得ln2<
<
<0.6934.
所以ln2的近似值为0.693.
| ex•e-x |
即f′(x)≥0,当且仅当ex=e-x即x=0时,f′(x)=0,
∴函数f(x)在R上为增函数.
(Ⅱ)g(x)=f(2x)-4bf(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,
则g′(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]
=2[(ex+e-x)2-2b(ex+e-x)+(4b-4)]
=2(ex+e-x-2)(ex+e-x+2-2b).
①∵ex+e-x≥2,ex+e-x+2≥4,
∴当2b≤4,即b≤2时,g′(x)≥0,当且仅当x=0时取等号,
从而g(x)在R上为增函数,而g(0)=0,
∴x>0时,g(x)>0,符合题意.
②当b>2时,若x满足2<ex+e-x<2b-2即
|
| b2-2b |
又由g(0)=0知,当0<x≤ln(b-1+
| b2-2b |
综合①、②知,b≤2,得b的最大值为2.
(Ⅲ)∵1.4142<
| 2 |
为了凑配ln2,并利用
| 2 |
| 2 |
| 1 |
| 2 |
得g(ln
| 2 |
| 3 |
| 2 |
| 2 |
当b=2时,由g(x)>0,得g(ln
| 2 |
| 3 |
| 2 |
| 2 |
从而ln2>
8
| ||
| 12 |
| 8×1.4142-3 |
| 12 |
令ln(b-1+
| b2-2b |
| 2 |
3
| ||
| 4 |
| b2-2b |
由g(x)<0,得g(ln
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
18+
| ||
| 28 |
| 18+1.4143 |
| 28 |
所以ln2的近似值为0.693.
点评:1.本题三个小题的难度逐步增大,考查了学生对函数单调性深层次的把握能力,对思维的要求较高,属压轴题.
2.从求解过程来看,对导函数解析式的合理变形至关重要,因为这直接影响到对导数符号的判断,是解决本题的一个重要突破口.
3.本题的难点在于如何寻求ln2,关键是根据第(2)问中g(x)的解析式探究b的值,从而获得不等式,这样自然地将不等式放缩为
的范围的端点值,达到了估值的目的.
2.从求解过程来看,对导函数解析式的合理变形至关重要,因为这直接影响到对导数符号的判断,是解决本题的一个重要突破口.
3.本题的难点在于如何寻求ln2,关键是根据第(2)问中g(x)的解析式探究b的值,从而获得不等式,这样自然地将不等式放缩为
| 2 |

练习册系列答案
相关题目
 如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.
如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.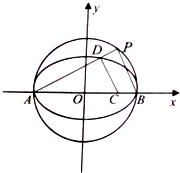 已知椭圆E:
已知椭圆E: