Question

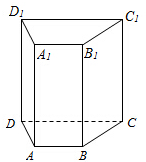如图，直四棱柱ABCD-A₁B₁C₁D₁，底面ABCD为梯形AB∥CD，ABC=90°，BC=CD=2AB=2．
（1）若CC₁=2，E为CD₁的中点，在侧面ABB₁A₁内是否存在点F，使EF⊥平面ACD₁，若存在，请确定点F的位置；若不存在，请说明理由；
（2）令点K为BB₁的中点，平面D₁AC与平面ACK所成锐二面角为60°，求DD₁的长．

Answer 1

考点：点、线、面间的距离计算,直线与平面垂直的判定

专题：综合题,空间位置关系与距离,空间角

分析：（1）以B为原点，BC，BA，BB₁分别为x，y，z轴，建立坐标系，若存在这样的点F，则可设F（0，y，z），其中0≤y≤1，0≤z≤2，利用EF⊥平面ACD₁，求出y=-3，z=5，与0≤y≤1，0≤z≤2矛盾，即可得出结论；
（2）设|DD₁|=2k（k＞0），求出平面ACK的法向量、平面ACD₁的法向量，利用向量的夹角公式，结合平面D₁AC与平面ACK所成锐二面角为60°，求出k，即可求DD₁的长．

解答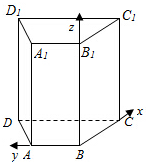： 解：（1）以B为原点，BC，BA，BB₁分别为x，y，z轴，建立坐标系，
则A（0，1，0），B（0，0，0），C（2，0，0），D₁（2，2，2），
若存在这样的点F，则可设F（0，y，z），其中0≤y≤1，0≤z≤2，

EF

=（-2，y-1，z-1），

AC

=（2，-1，0），

CD1

=（0，2，2），
∵EF⊥平面ACD₁，
∴

-4-(y-1)=0 2(y-1)+2(z-1)=0

，∴y=-3，z=5，
与0≤y≤1，0≤z≤2矛盾，
∴不存在满足条件的点F；
（2）设|DD₁|=2k（k＞0），则K（0，0，k），D₁（2，2，2k），

AK

=（0，-1，k），

AD1

=（2，1，2k），
设平面ACK的法向量为

m

=（x，y，z），则

-y+kz=0 2x-y=0

，
取

m

=（k，2k，2），
同理平面ACD₁的法向量为

n

=（-k，-2k，2），
则

|-k2-4k2+4|

5k2+4 • 5k2+4

=

1

2

∴k=±

2 15

15

或±

2 15

5

（负值舍去），
∴DD₁的长为

2 15

15

或

4 15

5

．

点评：本题考查直线与平面垂直的判定，考查向量知识的运用，正确求出平面的法向量是关键．