题目内容
已知函数g(x)=
,f(x)=g(x)-ax.
(Ⅰ)求函数g(x)的单调区间;
(Ⅱ)若函数f(x)在(1,+∞)上是减函数,求实数a的最小值;
(Ⅲ)若?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,求实数a的取值范围.
| x |
| lnx |
(Ⅰ)求函数g(x)的单调区间;
(Ⅱ)若函数f(x)在(1,+∞)上是减函数,求实数a的最小值;
(Ⅲ)若?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,求实数a的取值范围.
考点:利用导数求闭区间上函数的最值,导数的运算,利用导数研究函数的单调性
专题:导数的综合应用
分析:(I)利用导数的运算法则可得g′(x),分别解出g′(x)>0,g′(x)<0,即可得出其单调区间;
(II)函数f(x)在(1,+∞)上是减函数,可得f′(x)≤0恒成立,即
≤0恒成立.通过分离参数转化为a≥[
-
]max.,再利用二次函数的单调性即可得出;
(III))由于?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,可得g(x1)max≤[f′(x2)+2a]max.分别利用导数和二次函数的单调性即可得出.
(II)函数f(x)在(1,+∞)上是减函数,可得f′(x)≤0恒成立,即
| lnx-1-a(lnx)2 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| (lnx)2 |
(III))由于?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,可得g(x1)max≤[f′(x2)+2a]max.分别利用导数和二次函数的单调性即可得出.
解答:
解:(I)g′(x)=
(x>0且x≠1).
令g′(x)>0,解得,x>e,因此函数g(x)在区间(e,+∞)单调递增;
令g′(x)<0,解得0<x<e且x≠1,因此函数g(x)在区间(0,1),(1,e)单调递减.
(II)f(x)=g(x)-ax=
-ax(x>1).f′(x)=
.
∵函数f(x)在(1,+∞)上是减函数,∴f′(x)≤0恒成立,即
≤0恒成立.
∴a≥[
-
]max.
∵x>1,∴lnx>0,
∴
-
=-(
-
)2+
≤
,当lnx=2,即x=e2时取等号.
∴a≥
.
∴实数a的最小值是
.
(III)∵?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,
∴g(x1)max≤[f′(x2)+2a]max.
由(I)可知:g(x1)在[e,e2]上单调递增,∴g(x1)max=g(e2)=
.
∵x∈[e,e2],∴1≤lnx≤2,∴
≤
≤1.
令h(x)=f′(x)+2a=
-a+2a=
-
+a=-(
-
)2+a≤a.
∴a≥
.
∴实数a的取值范围是[
,+∞).
| lnx-1 |
| (lnx)2 |
令g′(x)>0,解得,x>e,因此函数g(x)在区间(e,+∞)单调递增;
令g′(x)<0,解得0<x<e且x≠1,因此函数g(x)在区间(0,1),(1,e)单调递减.
(II)f(x)=g(x)-ax=
| x |
| lnx |
| lnx-1-a(lnx)2 |
| (lnx)2 |
∵函数f(x)在(1,+∞)上是减函数,∴f′(x)≤0恒成立,即
| lnx-1-a(lnx)2 |
| (lnx)2 |
∴a≥[
| 1 |
| lnx |
| 1 |
| (lnx)2 |
∵x>1,∴lnx>0,
∴
| 1 |
| lnx |
| 1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴a≥
| 1 |
| 4 |
∴实数a的最小值是
| 1 |
| 4 |
(III)∵?x1∈[e,e2],?x2∈[e,e2],使g(x1)≤f′(x2)+2a成立,
∴g(x1)max≤[f′(x2)+2a]max.
由(I)可知:g(x1)在[e,e2]上单调递增,∴g(x1)max=g(e2)=
| e2 |
| 2 |
∵x∈[e,e2],∴1≤lnx≤2,∴
| 1 |
| 2 |
| 1 |
| lnx |
令h(x)=f′(x)+2a=
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
∴a≥
| e2 |
| 2 |
∴实数a的取值范围是[
| e2 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性,考查了恒成立问题的等价转化方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
函数y=x3-ax在x=1处的切线与直线x-2y=0垂直,则a的值为( )
| A、5 | ||
B、
| ||
| C、3 | ||
D、
|
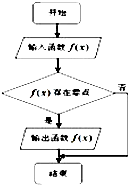 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: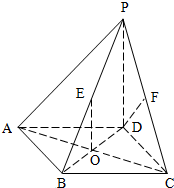 已知在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PD⊥平面ABCD,且PD=2,O为底面对角线的交点,E、F分别为棱PB,PC的中点
已知在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PD⊥平面ABCD,且PD=2,O为底面对角线的交点,E、F分别为棱PB,PC的中点