题目内容
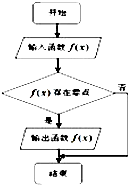 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数:①y=2x;
②y=2-x;
③f(x)=x+
| 1 |
| x |
④f(x)=x-
| 1 |
| x |
则输出函数的序号为( )
| A、① | B、② | C、③ | D、④ |
考点:程序框图
专题:计算题,算法和程序框图
分析:根据题意,得该程序框图输出的函数应满足存在零点,由此判定各选项中的函数是否满足条件即可.
解答:
解:模拟程序框图的运行过程,得该程序框图输出的函数应满足存在零点.
①y=2x>0,②y=2-x>0,③f(x)=x+
∈(-∞,-1]∪[1,+∞),故不存在零点;
④f(x)=x-
存在零点x=±1.
故选:D.
①y=2x>0,②y=2-x>0,③f(x)=x+
| 1 |
| x |
④f(x)=x-
| 1 |
| x |
故选:D.
点评:本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,得出解题的关键是输出的函数应满足的条件,是基础题.

练习册系列答案
相关题目
已知数列{an}的前n项之和Sn=n2-4n+1,则|a1|+|a2|+…+|a10|的值为( )
| A、61 | B、65 | C、67 | D、68 |
△ABC的内角A、B、C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,9b=10acosC,则sinA:sinB:sinC为( )
| A、4:3:2 |
| B、5:6:7 |
| C、5:4:3 |
| D、6:5:4 |
已知⊙C:(x-2)2+(y-1)2=4,直线l:y=-x+1,则l被⊙C所截得的弦长为( )
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
南宁市十二路公共汽车每5分钟一趟,某位同学每天乘十二路公共汽车上学,则他等车时间小于3分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=2x-1的值域是( )
| A、(0,+∞) | ||
| B、(-1,+∞) | ||
| C、(1,+∞) | ||
D、(
|
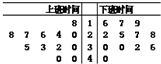 某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图如图,则上班、下班时间行驶速度的中位数分别是( )
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图如图,则上班、下班时间行驶速度的中位数分别是( )| A、28、27.5 |
| B、28、28.5 |
| C、29、27.5 |
| D、29、28.5 |