题目内容
函数y=x3-ax在x=1处的切线与直线x-2y=0垂直，则a的值为（ ）
| A、5 | ||
B、
| ||
| C、3 | ||
D、
|
考点：利用导数研究曲线上某点切线方程,直线的一般式方程与直线的垂直关系
专题：计算题,导数的概念及应用
分析：由题意可得f′（1）=-2，解方程可求a．
解答：
解：∵y=x3-ax，
∴y′=3x2-a，
∵函数在x=1处的切线与直线x-2y=0垂直，
∴f′（1）=-2，即3-a=-2，解得a=5．
故选：A．
∴y′=3x2-a，
∵函数在x=1处的切线与直线x-2y=0垂直，
∴f′（1）=-2，即3-a=-2，解得a=5．
故选：A．
点评：本题考查导数的几何意义，考查直线的位置关系，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项之和Sn=n2-4n+1，则|a1|+|a2|+…+|a10|的值为（ ）
| A、61 | B、65 | C、67 | D、68 |
函数y=2x-1的值域是（ ）
| A、（0，+∞） | ||
| B、（-1，+∞） | ||
| C、（1，+∞） | ||
D、（
|
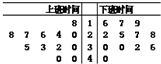某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图如图，则上班、下班时间行驶速度的中位数分别是（ ）| A、28、27.5 |
| B、28、28.5 |
| C、29、27.5 |
| D、29、28.5 |
已知α为第四象限角，且tanα=-2，则sinα=（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
函数f（x）=2sin2x（x∈R）是（ ）
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |