题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，C=
，a=2，b=3，求△ABC的周长及其外接圆的面积．
| π |
| 3 |
考点：正弦定理
专题：三角函数的求值
分析：利用余弦定理列出关系式，将a，b，cosC的值代入求出c的值，确定出三角形ABC周长，由正弦定理列出关系式，将c，sinC的值代入求出三角形ABC外接圆半径R，即可确定出外接圆面积．
解答：
解：∵在△ABC中，C=
，a=2，b=3，
∴由余弦定理得：c2=a2+b2-2abcosC=4+9-6=7，
解得：c=
，
∴△ABC周长为5+
；
令△ABC的外接圆的半径为R，由正弦定理得：2R=
=
，
解得：R=
，
则△ABC的外接圆的面积为S=
．
| π |
| 3 |
∴由余弦定理得：c2=a2+b2-2abcosC=4+9-6=7，
解得：c=
| 7 |
∴△ABC周长为5+
| 7 |
令△ABC的外接圆的半径为R，由正弦定理得：2R=
| c |
| sinC |
| ||||
|
2
| ||
| 3 |
解得：R=
| ||
| 3 |
则△ABC的外接圆的面积为S=
| 7π |
| 3 |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
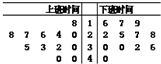某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图如图，则上班、下班时间行驶速度的中位数分别是（ ）| A、28、27.5 |
| B、28、28.5 |
| C、29、27.5 |
| D、29、28.5 |