题目内容
说明y=2sin(2x-
)+1的图象是由y=sinx的图象怎样变换而来的.
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:把y=sinx的图象向右平移
个单位,可得函数y=sin(x-
)的图象;
再把所得图象上的点的横坐标变为原来的
倍,纵坐标不变,可得函数y=sin(2x-
)的图象;
再所得图象上的点的纵坐标变为原来的2倍,横坐标不变,可得函数y=2sin(2x-
)的图象;
再所得图象上的点都向上平移1个单位,可得函数y=2sin(2x-
)+1的图象.
| π |
| 6 |
| π |
| 6 |
再把所得图象上的点的横坐标变为原来的
| 1 |
| 2 |
| π |
| 6 |
再所得图象上的点的纵坐标变为原来的2倍,横坐标不变,可得函数y=2sin(2x-
| π |
| 6 |
再所得图象上的点都向上平移1个单位,可得函数y=2sin(2x-
| π |
| 6 |
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
△ABC的内角A、B、C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,9b=10acosC,则sinA:sinB:sinC为( )
| A、4:3:2 |
| B、5:6:7 |
| C、5:4:3 |
| D、6:5:4 |
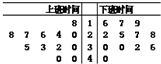 某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图如图,则上班、下班时间行驶速度的中位数分别是( )
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图如图,则上班、下班时间行驶速度的中位数分别是( )| A、28、27.5 |
| B、28、28.5 |
| C、29、27.5 |
| D、29、28.5 |
函数f(x)=2sin2x(x∈R)是( )
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |