题目内容

（1）已知椭圆的焦点在x轴上，长轴长为4，焦距为2，求椭圆的标准方程；
（2）已知双曲线的渐近线方程为y=±
3
4
x，准线方程为x=±
16
5
，求该双曲线的标准方程．
考点：双曲线的简单性质,椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）利用椭圆的标准方程及其性质即可得出；
（2）利用双曲线的标准方程及其性质即可得出．
解答： 解：（1）设椭圆的标准方程为：
x2
a2
+
y2
b2
=1(a＞b＞0)，
由题意得a=2，c=1，⇒b2=3，
∴所求椭圆的标准方程为
x2
4
+
y2
3
=1．
（2）由题意知双曲线标准方程为：
x2
a2
-
y2
b2
=1，（a，b＞0）．
∴
b
a
=
3
4
，
a2
c
=
16
5
，
又c2=a2+b2，解得a=4，b=3，
∴所求双曲线标准方程为
x2
16
-
y2
9
=1．
点评：本题考查了椭圆与双曲线的标准方程及其性质，属于基础题．
练习册系列答案
相关题目
已知奇函数y=f（x），且f（x）=f（x+4），f（1）=2，则f（2）+f（3）+f（4）=
 
．
点P在圆（x+6）2+（y-8）2=16上，点A（-1，0），B（1，0）则|PA|2+|PB|2的最小值为
 
．
已知函数f（x）=ax，求函数f（x）的反函数．
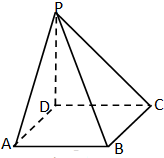四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥底面ABCD，PA=2AB，则四棱锥P-ABCD外接球的表面积为（　　）
A、24πB、8π
C、6πD、36π
若经过椭圆
x2
25
+
y2
16
=1的右焦点F2作垂直于x轴的直线与椭圆交于A、B两点，F1是椭圆的左焦点，则△AF1B的周长为（　　）
A、10B、20C、30D、40
5个学生的数学和物理成绩如表：
学生学科ABCDE
数学8075706560
物理7068666462
（1）画出散点图；
（2）求物理y与数学x之间的线性回归方程．
参考公式：回归直线的方程是：
y
=bx+a，其中b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
，a=
.
y
-b
.
x
，
y
i是与xi对应的回归估计值．
已知f（x），g（x），h（x）都是定义在R上的函数．若存在正实数m，n使得h（x）=mf（x）+ng（x）对任意的x∈R总成立，则称h（x）为函数f（x），g（x）在R上的“和生成”函数；若存在实数θ∈[0，π]，使得g（x）=f（x+θ）f（x）对任意的x∈R总成立，则称 g（x）是函数f（x）在R上的“积生成”函数；当P（x）=sin
x
2
，Q（x）=cos2x时，
（1）判断函数y=cos3x是否为函数P（x），Q（x）在R上的“和生成”函数，请说明理由；
（2）记L（x）为函数P（x），Q（x）在R上的一个“和生成”函数，若L（
π
3
）=1，且L（x）的最大值为4，求L（x）的解析式．
已知函数f（x）=[2sin（x+
π
3
）+sinx]cosx-
3
sin2x．
（1）若函数y=f（x）的图象关于直线x=a（a＞0）对称，求a的最小值；
（2）若函数y=mf（x）-2在x∈[0，
5π
12
]存在零点，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网