ƒøƒ⁄»ð
…ËŒÞ«Ó ˝¡–{an}£¨»Áπ˚¥Ê‘⁄≥£ ˝A£¨∂‘”⁄»Œ“‚∏¯∂®µƒ’˝ ˝?£®ŒÞ¬€∂ý–°£©£¨◊Хʑ⁄’˝’˚ ˝N£¨ πµ√n£æN ±£¨∫„”–|an-A|£º?≥…¡¢£¨æÕ≥∆ ˝¡–{an}µƒº´œÞŒ™A£¨‘ÚÀƒ∏ˆŒÞ«Ó ˝¡–£∫
¢Ÿ{£®-1£©n°¡2}£ª
¢⁄{
+
+
+°≠+
}£ª
¢€{1+
+
+
+°≠+
}£ª
¢Ð{1°¡2+2°¡22+3°¡23+°≠+n°¡2n}£¨
∆‰º´œÞŒ™2π≤”–£®°°°°£©
¢Ÿ{£®-1£©n°¡2}£ª
¢⁄{
| 1 |
| 1°¡3 |
| 1 |
| 3°¡5 |
| 1 |
| 5°¡7 |
| 1 |
| (2n-1)(2n+1) |
¢€{1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
¢Ð{1°¡2+2°¡22+3°¡23+°≠+n°¡2n}£¨
∆‰º´œÞŒ™2π≤”–£®°°°°£©
| A°¢4∏ˆ | B°¢3∏ˆ | C°¢2∏ˆ | D°¢1∏ˆ |
øºµ„£∫ ˝¡–µƒº´œÞ
◊®Ã‚£∫º∆À„Â,µ»≤Ó ˝¡–”ε»±» ˝¡–
∑÷Œˆ£∫∑÷±«Û∫Õ£¨‘Ÿ«Ûº´œÞ£¨º¥ø…µ√≥ˆΩ·¬€£Æ
Ω‚¥£∫
Ω‚£∫¢Ÿ ˝¡–{£®-1£©n°¡2} «∞⁄∂Ø ˝¡–£¨≤ª¥Ê‘⁄º´œÞ£ª
¢⁄
+
+
+°≠+
=
£®1-
+
-
+°≠+
-
£©=
£®1-
£©£¨ ˝¡–{an}µƒº´œÞŒ™
£ª
¢€{1+
+
+
+°≠+
}µƒº´œÞŒ™
=2£ª
¢ÐSn=1°¡2+2°¡22+3°¡23+°≠+n°¡2n°≠¢Ÿ£¨
2Sn=1•22+2•23+°≠+n•2n+1 °≠¢⁄£¨
°ý¢Ÿ-¢⁄µ√-Sn=21+22+23+°≠+2n-n•2n+1
°ý-Sn=2n+1-2-n°¡2n+1
°ýSn=£®n-1£©2n+1+2£¨
°ý ˝¡–{an}µƒº´œÞ≤ª¥Ê‘⁄£Æ
π —°£∫D£Æ
¢⁄
| 1 |
| 1°¡3 |
| 1 |
| 3°¡5 |
| 1 |
| 5°¡7 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
¢€{1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| 1 | ||
1-
|
¢ÐSn=1°¡2+2°¡22+3°¡23+°≠+n°¡2n°≠¢Ÿ£¨
2Sn=1•22+2•23+°≠+n•2n+1 °≠¢⁄£¨
°ý¢Ÿ-¢⁄µ√-Sn=21+22+23+°≠+2n-n•2n+1
°ý-Sn=2n+1-2-n°¡2n+1
°ýSn=£®n-1£©2n+1+2£¨
°ý ˝¡–{an}µƒº´œÞ≤ª¥Ê‘⁄£Æ
π —°£∫D£Æ
µ„∆¿£∫±æÂøº≤È ˝¡–µƒº´œÞ£¨øº≤È ˝¡–µƒ«Û∫Õ£¨’˝»∑«Û∫Õ «πÿº¸£Æ

¡∑œ∞≤·œµ¡–¥∞∏
 ”≈∞Ÿ∑÷øŒ ±ª•∂Øœµ¡–¥∞∏
”≈∞Ÿ∑÷øŒ ±ª•∂Øœµ¡–¥∞∏ ø™–ƒÕÐ◊¥‘™◊˜“µœµ¡–¥∞∏
ø™–ƒÕÐ◊¥‘™◊˜“µœµ¡–¥∞∏
œýπÿƒø

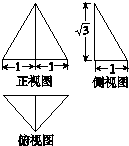 “ª∏ˆº∏∫ŒÃµƒ»˝ ”Õº»ÁÕºÀ˘ 棨∆‰÷–’˝ ”Õº «“ª∏ˆ’˝»˝Ω«–Œ£¨‘Ú’‚∏ˆº∏∫ŒÃµƒ±Ì√ʪ˝Œ™
“ª∏ˆº∏∫ŒÃµƒ»˝ ”Õº»ÁÕºÀ˘ 棨∆‰÷–’˝ ”Õº «“ª∏ˆ’˝»˝Ω«–Œ£¨‘Ú’‚∏ˆº∏∫ŒÃµƒ±Ì√ʪ˝Œ™