题目内容
设OA,OB,OC为不共面的三条射线,若∠AOB=∠AOC=60°,∠BOC=90°点P为射线OA上一点,设OP=a,则点P到平面OBC的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:作PH⊥平面BOC于H,连接OH.分别作HE⊥OB、HF⊥OC,交OB、OC于点E、F,连HE、HF,求出OH,即可求出点P到平面OBC的距离.
解答:
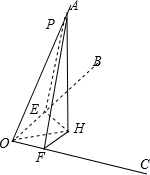 解:作PH⊥平面BOC于H,连接OH.分别作HE⊥OB、HF⊥OC,交OB、OC于点E、F,连HE、HF,则
解:作PH⊥平面BOC于H,连接OH.分别作HE⊥OB、HF⊥OC,交OB、OC于点E、F,连HE、HF,则
易知HE⊥OB、HF⊥OC,
∵∠AOB=∠AOC=60°,OP=a,
∴OE=OF=
,
∵∠BOC=90°,
∴OH=
a,
∴PH=
=
a,
∴点P到平面OBC的距离为
a.
故选:A.
 解:作PH⊥平面BOC于H,连接OH.分别作HE⊥OB、HF⊥OC,交OB、OC于点E、F,连HE、HF,则
解:作PH⊥平面BOC于H,连接OH.分别作HE⊥OB、HF⊥OC,交OB、OC于点E、F,连HE、HF,则易知HE⊥OB、HF⊥OC,
∵∠AOB=∠AOC=60°,OP=a,
∴OE=OF=
| a |
| 2 |
∵∠BOC=90°,
∴OH=
| ||
| 2 |
∴PH=
a2-
|
| ||
| 2 |
∴点P到平面OBC的距离为
| ||
| 2 |
故选:A.
点评:本题考查点P到平面OBC的距离,考查学生的计算能力,正确求出OH是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
曲线y=2x3-6x上切线平行于x轴的点的坐标是( )
| A、(-1,4) |
| B、(1,-4) |
| C、(-1,-4)或(1,4) |
| D、(-1,4)或(1,-4) |
设tanα、tanβ是方程x2-9x+4=0的两个根,则tan(α+β)=( )
| A、-1 | B、3 | C、-3 | D、1 |
若复数(1+bi)(2-i)是纯虚数(b是实数,i是虚数单位),则b等于( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
已知三棱锥S-ABC的所有顶点都在球O的球面上,AB=BC=CA=3,SA=SB=SC,球心O到平面ABC的距离为1,则SA与平面ABC所成角的大小为( )
| A、30° |
| B、60° |
| C、30°或60° |
| D、45°或60° |
方程x2+y2-2x+4y+6=0表示的曲线是( )
| A、圆 | B、点 | C、不存在 | D、无法确定 |
双曲线
-
=1的焦距( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、10 | B、16 | C、20 | D、100 |
盒中有4个红球3个黄球,从中任取一个球,用X表示取出的黄球个数,那么DX等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=f(x)在R上有定义,对于任一给定的正数P,定义函数fp(x)=
,则称函数fp(x)为 f(x)的“P界函数”.若给定函数f(x)=x2-2x-1,p=2,则下列结论不成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、f[f(2)]=fp[fp(2)]? |
| D、f[f(3)]=fp[fp(3)]? |