题目内容
已知三棱锥S-ABC的所有顶点都在球O的球面上,AB=BC=CA=3,SA=SB=SC,球心O到平面ABC的距离为1,则SA与平面ABC所成角的大小为( )
| A、30° |
| B、60° |
| C、30°或60° |
| D、45°或60° |
考点:与二面角有关的立体几何综合题
专题:空间角
分析:由已知条件得OE=1,AE=
,OA=SO=
=2,SE=3,SA=2
,∠SAE是SA与平面ABC所成角,由此能求出结果.
| 3 |
| 3+1 |
| 3 |
解答:
解: 如图,三棱锥S-ABC的所有顶点都在球O的球面上,
如图,三棱锥S-ABC的所有顶点都在球O的球面上,
AB=BC=CA=3,SA=SB=SC,球心O到平面ABC的距离为1,
∴OE=1,AE=
=
,
∴OA=SO=
=2,
∴SE=3,SA=
=2
,
∵SE⊥面ABC,
∴∠SAE是SA与平面ABC所成角,
∵cos∠SAE=
=
=
,
∴∠SAE=60°.
当球心不在三棱锥内时,
同理解得∠SAE=30°.
故选:C.
 如图,三棱锥S-ABC的所有顶点都在球O的球面上,
如图,三棱锥S-ABC的所有顶点都在球O的球面上,AB=BC=CA=3,SA=SB=SC,球心O到平面ABC的距离为1,
∴OE=1,AE=
| 2 |
| 3 |
9-
|
| 3 |
∴OA=SO=
| 3+1 |
∴SE=3,SA=
| 9+3 |
| 3 |
∵SE⊥面ABC,
∴∠SAE是SA与平面ABC所成角,
∵cos∠SAE=
| AE |
| SA |
| ||
2
|
| 1 |
| 2 |
∴∠SAE=60°.
当球心不在三棱锥内时,
同理解得∠SAE=30°.
故选:C.
点评:本题考查线面角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
从学号为0~50的燕中高二某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A、1,2,3,4,5 |
| B、5,16,27,38,49 |
| C、2,4,6,8,10 |
| D、4,13,22,31,40 |
函数y=
的图象如图所示,则( )
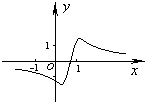
| 2(x+a) |
| (x+a)2+b |

| A、a∈(0,1),b∈(0,1) |
| B、a∈(0,1),b∈(1,+∞) |
| C、a∈(-1,0),b∈(1,+∞) |
| D、a∈(-1,0),b∈(0,1) |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行;
②若两个平面都垂直于同一条直线,则这两个平面平行;
③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;
④两个平行直线能确定一个平面,其中正确的命题是( )
①若一个平面内的两条直线与另一个平面都平行,则这两个平面平行;
②若两个平面都垂直于同一条直线,则这两个平面平行;
③若两个平面互相垂直,则在其中一个平面内的直线垂直另外一个平面;
④两个平行直线能确定一个平面,其中正确的命题是( )
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
下列函数中,最小正周期为π的是( )
| A、y=|sinx| | ||
| B、y=sinx | ||
C、y=tan
| ||
| D、y=cos4x |
设OA,OB,OC为不共面的三条射线,若∠AOB=∠AOC=60°,∠BOC=90°点P为射线OA上一点,设OP=a,则点P到平面OBC的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=sinωx的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
 如图,已知向量
如图,已知向量| p |
| q |
| π |
| 4 |
| p |
| 2 |
| q |
| AB |
| p |
| q |
| AC |
| p |
| q |
| AD |
A、
| ||||
B、
| ||||
| C、7 | ||||
| D、18 |