题目内容
已知函数f(x)=-x2+2ex+m-1,g(x)=x+
(x>0).
(1)若y=g(x)-m有零点,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
| e2 |
| x |
(1)若y=g(x)-m有零点,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
考点:函数零点的判定定理,根的存在性及根的个数判断
专题:计算题,函数的性质及应用,导数的综合应用,不等式的解法及应用
分析:(1)由基本不等式可得g(x)=x+
≥2
=2e,从而求m的取值范围;
(2)令F(x)=g(x)-f(x)=x+
+x2-2ex-m+1,求导F′(x)=1-
+2x-2e=(x-e)(
+2);从而判断函数的单调性及最值,从而确定m的取值范围.
| e2 |
| x |
x•
|
(2)令F(x)=g(x)-f(x)=x+
| e2 |
| x |
| e2 |
| x2 |
| x+e |
| x2 |
解答:
解:(1)∵g(x)=x+
≥2
=2e;
(当且仅当x=
,即x=e时,等号成立)
∴若使函数y=g(x)-m有零点,
则m≥2e;
故m的取值范围为[2e,+∞);
(2)令F(x)=g(x)-f(x)
=x+
+x2-2ex-m+1,
F′(x)=1-
+2x-2e=(x-e)(
+2);
故当x∈(0,e)时,F′(x)<0,x∈(e,+∞)时,F′(x)>0;
故F(x)在(0,e)上是减函数,在(e,+∞)上是增函数,
故只需使F(e)<0,
即e+e+e2-2e2-m+1<0;
故m>2e-e2+1.
| e2 |
| x |
x•
|
(当且仅当x=
| e2 |
| x |
∴若使函数y=g(x)-m有零点,
则m≥2e;
故m的取值范围为[2e,+∞);
(2)令F(x)=g(x)-f(x)
=x+
| e2 |
| x |
F′(x)=1-
| e2 |
| x2 |
| x+e |
| x2 |
故当x∈(0,e)时,F′(x)<0,x∈(e,+∞)时,F′(x)>0;
故F(x)在(0,e)上是减函数,在(e,+∞)上是增函数,
故只需使F(e)<0,
即e+e+e2-2e2-m+1<0;
故m>2e-e2+1.
点评:本题考查了基本不等式的应用及导数的综合应用,同时考查了函数零点的判断与应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知i是虚数单位,若z(1+3i)=i,则z的虚部为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
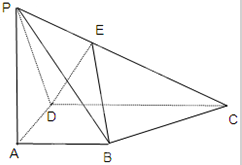 如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45°
如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45° 在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点.
在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点. 已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.
已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.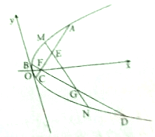 如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且
如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且