题目内容
已知|z+2-2i|=1，求|z|的最值．
考点：复数求模
专题：数系的扩充和复数
分析：把已知的等式变形，由其几何意义画出图形得答案．
解答：
解：由|z+2-2i|=1，得|z-（-2+2i）|=1，
即复数z在复平面内对应的点在以（-2，2）为圆心，以1为半径的圆周上，
如图，
则|z|的最大值为2
+1，最小值为2
-1．
即复数z在复平面内对应的点在以（-2，2）为圆心，以1为半径的圆周上，
如图，
则|z|的最大值为2
| 2 |
| 2 |
点评：本题考查了复数模的求法，关键是对|z+2-2i|=1的几何意义的理解，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知空间中的直线l和两个不同的平面α、β，且l?α，l?β．若α⊥β，则命题p：“l⊥β”是命题q：“l∥α”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设p：x∈{x|y=lg（x-1）}，q：x∈{x|2-x＜1}，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i是虚数单位，若z（1+3i）=i，则z的虚部为（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
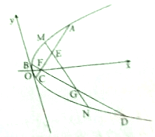如图，已知抛物线C：y2=2px（p＞0）的焦点F（1，0）过点F作任何两条弦AC，BD，且