题目内容
已知椭圆
+y2=1,过椭圆左焦点F1作倾斜角为60°的直圆交于CD两点,A2为椭圆的右顶点,求△CDA2的面积.
| x2 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:求出CD的方程,代入 x2+2y2=2 求得交点C,D的坐标,再利用两点之间的距离公式即可得出|CD|=
.利用点到直线的距离公式可得点A2到直线CD的距离d,即可得出S=
•|CD|•d,
| (x1-x2)2+(y1-y2)2 |
| 1 |
| 2 |
解答:
解:椭圆
+y2=1,过椭圆左焦点F1(-1,0),作倾斜角为60°的直圆交于CD两点,
CD的方程为:y=
x+
,
把 y=
x+
代入 x2+2y2=2 得7x2+12x+4=0,
解得x1+x2=-
,x1x2=
,
∴|CD|=
=
|x1-x2|=2
=
.
点A2(
,0)到直线CD的距离d=
=
,
△CDA2的面积S=
•|CD|•d=
×
×
=
.
| x2 |
| 2 |
CD的方程为:y=
| 3 |
| 3 |
把 y=
| 3 |
| 3 |
解得x1+x2=-
| 12 |
| 7 |
| 4 |
| 7 |
∴|CD|=
| (x1-x2)2+(y1-y2)2 |
| 1+3 |
(-
|
8
| ||
| 7 |
点A2(
| 2 |
|
| ||||
|
| ||||
| 2 |
△CDA2的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
8
| ||
| 7 |
| ||||
| 2 |
2(
| ||||
| 7 |
点评:本题考查了直线与椭圆相交问题、椭圆的标准方程及其性质、两点之间的距离公式、三角形的面积计算公式,考查了计算能力,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点.
在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点.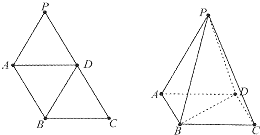 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(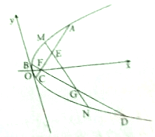 如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且
如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且