题目内容
已知函数y=-3x2-12x+1，x∈（-∞，-2），判断该函数的单调性并证明．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：①根据函数y=f（x）是二次函数，对称轴是x=-2，得出f（x）在x∈（-∞，-2）时是增函数；
②利用函数的单调性定义证明f（x）在x∈（-∞，-2）时是增函数即可．
②利用函数的单调性定义证明f（x）在x∈（-∞，-2）时是增函数即可．
解答：
解：①函数y=f（x）=-3x2-12x+1是二次函数，图象是抛物线，且开口向下，对称轴是x=-2；
在对称轴的右侧，函数f（x）是增函数；
∴函数f（x）在x∈（-∞，-2）时是增函数；
②证明：任取x1、x2∈（-∞，-2），且x1＜x2；
∴f（x1）-f（x2）=（-3x12-12x1+1）-（-3x22-12x2+1）=3（x2-x1）（x1+x2+4）；
∵x1＜x2＜-2，∴x2-x1＞0，x1+x2+4＜0，
∴f（x1）＜f（x2）；
∴函数y=f（x）在x∈（-∞，-2）时是增函数．
在对称轴的右侧，函数f（x）是增函数；
∴函数f（x）在x∈（-∞，-2）时是增函数；
②证明：任取x1、x2∈（-∞，-2），且x1＜x2；
∴f（x1）-f（x2）=（-3x12-12x1+1）-（-3x22-12x2+1）=3（x2-x1）（x1+x2+4）；
∵x1＜x2＜-2，∴x2-x1＞0，x1+x2+4＜0，
∴f（x1）＜f（x2）；
∴函数y=f（x）在x∈（-∞，-2）时是增函数．
点评：本题考查了二次函数的单调性及其证明问题，解题时应根据二次函数的图象与性质判断其单调性，再利用函数的单调性进行证明，是基础题．
练习册系列答案
相关题目
已知随机变量X服从正态分布N（1，4），且P（0≤X≤2）=0.68，则P（X＞2）=（ ）
| A、0.34 | B、0.16 |
| C、0.84 | D、0.32 |
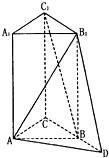已知正三棱柱ABC-A1B1C1中，AA1=2AC=4，延长CB至D，使CB=BD．
如图，圆周上有n个固定点，分别为A1，A2，…，An（n∈N*，n≥2），在每一个点上分别标上1，2，3中的某一个数字，但相邻的两个数字不相同，记所有的标法总数为an．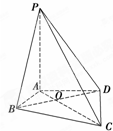
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=∠ADC=90°，∠BAD=120°，AD=AB=1，AC交BD于O点．