题目内容
17.若方程x2+$\frac{{y}^{2}}{a}$=1(a是常数),则下列结论正确的是( )| A. | 任意实数a方程表示椭圆 | B. | 存在实数a方程表示椭圆 | ||
| C. | 任意实数a方程表示双曲线 | D. | 存在实数a方程表示抛物线 |
分析 根据三种圆锥曲线的定义,结合举例可得选项.
解答 解:对于a=1,方程x2+$\frac{{y}^{2}}{a}$=1表示圆,选项A错误;
当a>0且a≠1时,方程x2+$\frac{{y}^{2}}{a}$=1表示椭圆,B正确;
当a<0时,方程x2+$\frac{{y}^{2}}{a}$=1表示双曲线,C错误;
对于任意实数a,方程x2+$\frac{{y}^{2}}{a}$=1不是抛物线,D错误.
故选:B.
点评 本题考查曲线与方程,考查了三种圆锥曲线的定义,是基础题.

练习册系列答案
相关题目
7.下列四个式子中是恒等式的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α+β)=cosαcosβ+sinβsinβ | ||
| C. | tan(α+β)=$\frac{tanα-tanβ}{1-tanαtanβ}$ | D. | sin(α+β)sin(α-β)=sin2α-sin2β |
12.已知具有线性相关的两个变量x,y之间的一组数据如表:
且回归方程是$\stackrel{∧}{y}$=0.95x+2.6,则t=( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 2.5 | B. | 3.5 | C. | 4.5 | D. | 5.5 |
2.已知α为锐角,且$tanα=\sqrt{2}-1$,函数$f(x)={x^2}tan2α+x•sin(2α+\frac{π}{4})$,数列{an}的首项${a_1}=\frac{1}{2}\;,\;{a_{n+1}}=f({a_n})$,则有( )
| A. | an+1>an | B. | an+1≥an | C. | an+1<an | D. | an+1≤an |
9.设i为虚数单位,则复数$\frac{1-i}{i}$的共轭复数所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
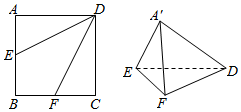 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′. 如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.
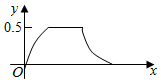
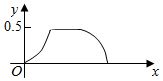
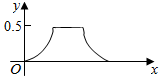
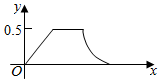
如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.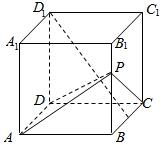 在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )
在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )