题目内容
复平面内关于原点对称的两点对应的复数为z1，z2，且满足3z1+（z2-2）i=2z2-（1+z1）i，求z1，z2的值．
考点：复数代数形式的乘除运算
专题：计算题,数系的扩充和复数
分析：设z1=a+bi（a，b∈R），则z2=-a-bi，代入等式化简，由复数相等的条件可得方程组，解出即可．
解答：
解：设z1=a+bi（a，b∈R），则z2=-a-bi，
代入等式得，3（a+bi）+（-a-bi-2）i=2（-a-bi）-（1+a+bi）i，
化简得3a+b+（3b-a-2）i=b-2a-（2b+a+1）i，
∴
，即
，解得
，
∴z1=
i，z2=-
i．
代入等式得，3（a+bi）+（-a-bi-2）i=2（-a-bi）-（1+a+bi）i，
化简得3a+b+（3b-a-2）i=b-2a-（2b+a+1）i，
∴
|
|
|
∴z1=
| 1 |
| 5 |
| 1 |
| 5 |
点评：该题考查复数代数形式的乘除运算、复数相等的充要条件，属基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
函数f（x）=2x3+3x-3的零点所在的区间为（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
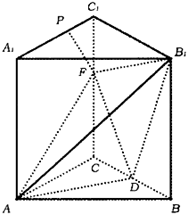在直三棱柱ABC-A1B1C1中，AB=AC═3，BC=2，D是BC的中点，F是上一点，且CF=2．
如图，BC为圆O的直径，D为圆周上异于B、C的一点，AB垂直于圆O所在的平面，BE⊥AC于点E，BF⊥AD于点F．