题目内容
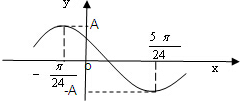已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-| π |
| 24 |
| 11π |
| 24 |
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2014π |
| 8 |
| 2014 |
 |
| i=1 |
| i•π |
| 8 |
| A、0 | ||
B、-1-
| ||
| C、-1 | ||
D、-1+
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：根据直线y=A与曲线y=f（x）（-
≤x≤
）所围成的封闭图形的面积为π求出A，根据最大值和最小值的距离求得函数的最小正周期进而求得ω，结合最大值点，求得相位φ，则函数解析式可得．结合函数的周期性，代入可得答案．
| π |
| 24 |
| 11π |
| 24 |
解答：
解：由已知可得函数f（x）的周期为
，
∵ω＞0得：ω=4，
又∵直线y=A与曲线y=f（x）（-
≤x≤
）所围成的封闭图形的面积为π，
故π=
×
×2A，
由A＞0得：A=2，
又∵函数f（x）的图象过（-
，2）点，
故4×-
+φ=
+2kπ，k∈Z，
则φ=
+2kπ，k∈Z，
又∵0＜φ＜π，
故φ=
，
故f（x）=2sin（4x+
），
故f（
）以4为周期呈周期变化，且每个周期内的和为0，
∵2014÷4=503…2，
故f（
）+f（
）+f（
）+…+f（
）=f（
）+f（
）=2sin（
+
）+2sin（π+
）=-2cos
-2sin
=-1-
，
故选：B
| π |
| 2 |
∵ω＞0得：ω=4，
又∵直线y=A与曲线y=f（x）（-
| π |
| 24 |
| 11π |
| 24 |
故π=
| 1 |
| 2 |
| π |
| 2 |
由A＞0得：A=2，
又∵函数f（x）的图象过（-
| π |
| 24 |
故4×-
| π |
| 24 |
| π |
| 2 |
则φ=
| 2π |
| 3 |
又∵0＜φ＜π，
故φ=
| 2π |
| 3 |
故f（x）=2sin（4x+
| 2π |
| 3 |
故f（
| i•π |
| 8 |
∵2014÷4=503…2，
故f（
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2014π |
| 8 |
| π |
| 8 |
| 2π |
| 8 |
| π |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
故选：B
点评：本题考查由y=Asin（ωx+φ）的部分图象求函数解析式，关键是掌握利用五点作图中的某一点求φ的值的方法，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
| ∫ |
0 |
| A、-1 | B、-2 | C、1 | D、3 |
等差数列数列{an}的公差为2，前n项和为Sn，若a1，a3，a4成等比数列，则S20=（ ）
| A、180 | B、220 |
| C、580 | D、410 |
下列关系属于线性负相关的是（ ）
| A、父母的身高与子女身高的关系 |
| B、身高与手长 |
| C、吸烟与健康的关系 |
| D、数学成绩与物理成绩的关系 |
设f（x）与g（x）是定义在同一区间[m，n]上的两个函数，若函数y=f（x）+g（x）在x∈[m，n]上有两个不同的零点，则称f（x）和g（x）在[m，n]上是“相互函数”；若f（x）=-4lnx-5x与g（x）=x2+3x+a在区间[1，e]上是相互函数，则a的取值范围为（ ）
| A、[1，4ln2） |
| B、[-e2+2e+4，4ln2） |
| C、（4ln2，+∞） |
| D、[1，-e2+2e+4] |
函数f（x）=2x3+3x-3的零点所在的区间为（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |