题目内容
已知函数f(x)=ex-e-x(x∈R),不等式et•f(2t)-mf(t)<0对于t∈(0,1)恒成立,则实数m的取值范围是 .
考点:函数恒成立问题,函数单调性的性质
专题:函数的性质及应用
分析:根据指数函数的性质,将不等式转化为求函数的最值恒成立问题,即可得到结论.
解答:
解:∵f(x)=ex-e-x(x∈R),
∴f(2x)=e2x-e-2x(x∈R),
则不等式et•f(2t)-mf(t)<0等价为
et•(e2t-e-2t)-m(et-e-t)<0,
即et•(et-e-t)(et+e-t)<m(et-e-t),
当t∈(0,1)时,et-e-t>0,
∴不等式等价为et•(et+e-t)<m,
即e2t+1<m在t∈(0,1)恒成立,
即(e2t+1)max<m,
当t∈(0,1)时,e2t+1∈(2,e2+1),
∴m≥e2+1,
故答案为:[e2+1,+∞).
∴f(2x)=e2x-e-2x(x∈R),
则不等式et•f(2t)-mf(t)<0等价为
et•(e2t-e-2t)-m(et-e-t)<0,
即et•(et-e-t)(et+e-t)<m(et-e-t),
当t∈(0,1)时,et-e-t>0,
∴不等式等价为et•(et+e-t)<m,
即e2t+1<m在t∈(0,1)恒成立,
即(e2t+1)max<m,
当t∈(0,1)时,e2t+1∈(2,e2+1),
∴m≥e2+1,
故答案为:[e2+1,+∞).
点评:本题主要考查指数函数的性质和运算,以及根据指数函数的性质解决不等式恒成立问题,考查学生的计算能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
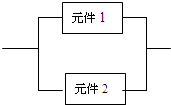 某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为
某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为