题目内容
已知三棱锥D-ABC中,AB=BC=1,AD=2,BD=
,AC=
,BC⊥AD,则三棱锥的外接球的体积为= .
| 5 |
| 2 |
考点:球内接多面体
专题:空间位置关系与距离
分析:根据勾股定理可判断AD⊥AB,AB⊥BC,从而可得三棱锥的各个面都为直角三角形,求出三棱锥的外接球的直径,即可求出三棱锥的外接球的体积.
解答:
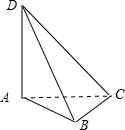 解:如图:∵AD=2,AB=1,BD=
解:如图:∵AD=2,AB=1,BD=
,满足AD2+AB2=SD2
∴AD⊥AB,又AD⊥BC,BC∩AB=B,
∴AD⊥平面ABC,
∵AB=BC=1,AC=
,∴AB⊥BC,∴BC⊥平面DAB,
∴CD是三棱锥的外接球的直径,
∵AD=2,AC=
,
∴CD=
,
∴三棱锥的外接球的体积为
(
)3=
π.
故答案为:
π.
 解:如图:∵AD=2,AB=1,BD=
解:如图:∵AD=2,AB=1,BD=| 5 |
∴AD⊥AB,又AD⊥BC,BC∩AB=B,
∴AD⊥平面ABC,
∵AB=BC=1,AC=
| 2 |
∴CD是三棱锥的外接球的直径,
∵AD=2,AC=
| 2 |
∴CD=
| 6 |
∴三棱锥的外接球的体积为
| 4π |
| 3 |
| ||
| 2 |
| 6 |
故答案为:
| 6 |
点评:本题考查了三棱锥的外接球的体积,关键是根据线段的数量关系判断CD是三棱锥的外接球的直径.

练习册系列答案
相关题目
已知
=(1,1,0),
=(-1,0,2),且k
+
与2
-
垂直,则k的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
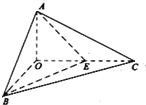 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.