题目内容
对于函数f(x),若f(1)=0,f(2)=3,f(3)=8,f(4)=15.运用归纳推理的方法可猜测f(n)= .
考点:归纳推理
专题:规律型
分析:已知中的函数值可转化为:f(1)=12-1,f(2)=22-1,f(3)=32-1,f(4)=42-1…,进而可归纳出f(n)的解析式.
解答:
解:∵f(1)=0,
f(2)=3,
f(3)=8,
f(4)=15,
可化为:
f(1)=12-1,
f(2)=22-1,
f(3)=32-1,
f(4)=42-1,
…,
∴可归纳出:f(n)=n2-1,
故答案为:n2-1
f(2)=3,
f(3)=8,
f(4)=15,
可化为:
f(1)=12-1,
f(2)=22-1,
f(3)=32-1,
f(4)=42-1,
…,
∴可归纳出:f(n)=n2-1,
故答案为:n2-1
点评:本题考查合情推理,考查了分析问题和解决问题的能力,解题的关键是找出函数值随自变量变化所呈现的规律.

练习册系列答案
相关题目
甲、乙、丙三人射击击中目标的概率分别为
,
,
.现在三人同时射击目标,则目标被击中的概率为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
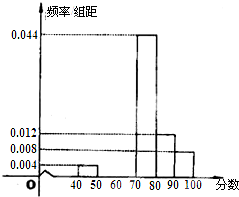 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员. 如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=