题目内容
曲线y2=x与y=x2所围成的图形的面积是 .
考点:定积分
专题:导数的概念及应用
分析:由题意,可作出两个函数y
=与y=x2的图象,由图象知阴影部分即为所求的面积,本题可用积分求阴影部分的面积,先求出两函数图象交点A的坐标,根据图象确定出被积函数-x2与积分区间[0,1],计算出定积分的值,即可出面积曲线y2=x,y=x2所围成图形的面积S.
| x |
解答:
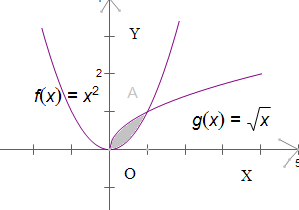 解:作出如图的图象
解:作出如图的图象
联立
解得,
或
即点A(1,1)
所求面积为:S=
(
-x2)dx=(
x
-
x3)
=
故答案为:
.
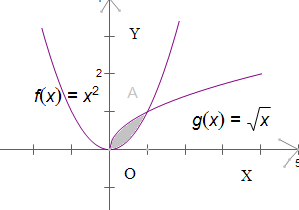 解:作出如图的图象
解:作出如图的图象联立
|
|
|
即点A(1,1)
所求面积为:S=
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查了定积分在求面积中的应用,会求一个函数的定积分,属于基础题.

练习册系列答案
相关题目
若抛物线y=ax2的焦点为F(0,1),则a的值为( )
A、
| ||
| B、4 | ||
C、
| ||
| D、2 |