题目内容
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
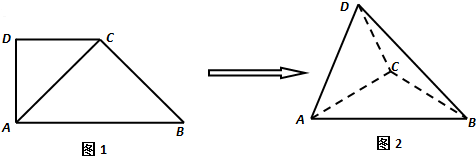
(Ⅰ)若E为AD的中点,试在线段CD上找一点F,使 EF∥平面ABC,并加以证明;
(Ⅱ)求证:BC⊥平面ACD;
(Ⅲ)求几何体A-BCD的体积.

(Ⅰ)若E为AD的中点,试在线段CD上找一点F,使 EF∥平面ABC,并加以证明;
(Ⅱ)求证:BC⊥平面ACD;
(Ⅲ)求几何体A-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)取DC的中点F,则F就是要确定的点,(2)由勾股定理证明BC⊥AC;(3)VA-BCD=VB-ACD
解答:
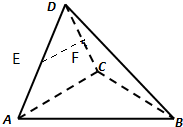 解:(Ⅰ)取DC的中点F,则F就是要确定的点,证明如下:
解:(Ⅰ)取DC的中点F,则F就是要确定的点,证明如下:
∵E为AD的中点,F是DC的中点,
∴EF∥AC,又EF在平面ABC外,AC在平面ABC内,
∴EF∥平面ABC.
(Ⅱ)证明:∵在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.
∴AC=
=2
,BC=
=2
,
∴AC2+BC2=16=AB2;
∴BC⊥AC,又∵平面ADC⊥平面ABC,
∴BC⊥平面ACD;
(Ⅲ)VA-BCD=VB-ACD=
×(
×2×2)×2
=
.
 解:(Ⅰ)取DC的中点F,则F就是要确定的点,证明如下:
解:(Ⅰ)取DC的中点F,则F就是要确定的点,证明如下:∵E为AD的中点,F是DC的中点,
∴EF∥AC,又EF在平面ABC外,AC在平面ABC内,
∴EF∥平面ABC.
(Ⅱ)证明:∵在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.
∴AC=
| 22+22 |
| 2 |
| 22+(4-2)2 |
| 2 |
∴AC2+BC2=16=AB2;
∴BC⊥AC,又∵平面ADC⊥平面ABC,
∴BC⊥平面ACD;
(Ⅲ)VA-BCD=VB-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
4
| ||
| 3 |
点评:本题考查了学生的空间想象力及作图能力,线面平行的判定定理及勾股定理.属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
若x+y=1(x,y>0),则
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
| A、1 | ||
| B、2 | ||
C、2
| ||
| D、4 |
 如图在棱长为1的正方体ABCD-A1B1C1D1中,点E为棱BC的中点,点F是棱CD上的动点.
如图在棱长为1的正方体ABCD-A1B1C1D1中,点E为棱BC的中点,点F是棱CD上的动点.