题目内容
在长方体ABCD﹣A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为( )
A. B.
B.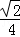 C.
C.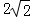 D.
D.
A
【解析】
试题分析:可以考虑用向量解决本题,所以分别以DA,DC,DD1三直线为x轴,y轴,z轴建立空间直角坐标系,根据线面角的概念知D1C1与平面A1BC1所成角的正弦值等于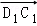 与平面A1BC1的法向量夹角的余弦值的绝对值,所以根据已知的边的长度求出
与平面A1BC1的法向量夹角的余弦值的绝对值,所以根据已知的边的长度求出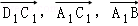 的坐标,设平面A1BC1的法向量为
的坐标,设平面A1BC1的法向量为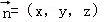 ,根据向量
,根据向量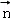 与
与 垂直即可求出
垂直即可求出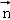 ,根据向量夹角余弦公式即可求出向量
,根据向量夹角余弦公式即可求出向量 ,
,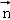 夹角的余弦值的绝对值.
夹角的余弦值的绝对值.
【解析】
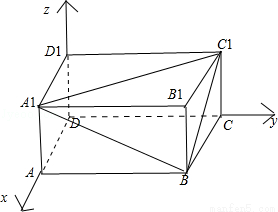
如图,分别以DA,DC,DD1三条边所在直线为x轴,y轴,z轴建立空间直角坐标系;
根据题意知,D1C1与平面A1BC1所成角的正弦值等于向量 和平面A1BC1的法向量夹角余弦值的绝对值;
和平面A1BC1的法向量夹角余弦值的绝对值;
根据已知的边的长度,可求以下几点坐标:
D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0);
∴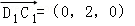 ,
,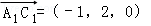 ,
,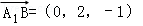 ;
;
设平面A1BC1的法向量为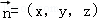 ,则
,则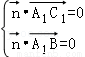 ;
;
∴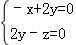 ,取y=1,∴
,取y=1,∴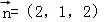 ;
;
∴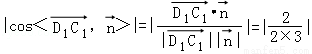 =
= .
.
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
(sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )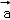 =(1,λ,2),
=(1,λ,2),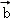 =(﹣2,1,1),
=(﹣2,1,1),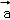 ,
,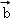 夹角的余弦值为
夹角的余弦值为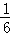 ,则λ等于( )
,则λ等于( )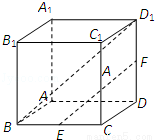
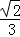 B.
B.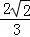 C.
C.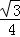 D.
D.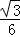
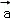 ,
,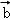 ,
,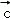 }是空间的一组单位正交基底,而{
}是空间的一组单位正交基底,而{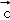 ,
, +
+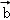 }是空间的另一组基底.若向量
}是空间的另一组基底.若向量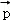 在基底{
在基底{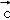 ,
,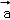 +
+ }下的坐标为( )
}下的坐标为( )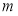 ,
,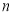 是两条不同直线,
是两条不同直线,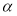 ,
,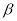 是两个不同的平面,且
是两个不同的平面,且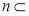
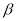 ,则下列叙述正确的是
,则下列叙述正确的是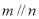 ,
,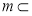
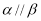
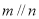
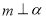 ,则
,则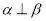
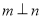 ,则
,则