题目内容
5.随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也在不断提高.某村村委会统计了2011到2015年五年间每年春节期间外出旅游的家庭数,具体统计数据如表所示:| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 18 | 22 | 26 |
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\widehat y$=bx+a,
并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的直线方程估计该村2018年在春节期间外出游泳的家庭数.
参考:用最小二乘法求线性回归方程系数公式$\widehat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\widehat a=\overline y-\widehat b\overline x$.
分析 (1)使用列举法求出所有基本事件的个数和至少有一年多余20人的事件数,使用古典概型的概率公式求出概率;
(2)根据相关系数公式求出相关系数,得出回归方程;
(3)将x=2018代入回归方程计算.
解答 解:(1)从这5年中任意抽取两年,所有的事件有:
(2011,2012),(2011,2013),(2011,2014),(2011,2015),(2012,2013),
(2012,2014),(2012,2015),(2013,2014),(2013,2015),(2014,2015)共10种,
至少有1年多于20人的事件有:
(2011,2014),(2011,2015),(2012,2014),(2012,2015),
(2013,2014),(2013,2015),(2014,2015)共7种,
则至少有1年多于10人的概率为P=$\frac{7}{10}$.
(2)由已知数据得$\overline{x}$=2013,$\overrightarrow{y}$=16,
$\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=-2×(-10)+(-1)×(-6)+1×6+2×10=52,
$\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}$=(-1)2+(-2)2+12+22=10,
∴$\stackrel{∧}{b}$=$\frac{52}{10}=5.2$,$\stackrel{∧}{a}$=16-5.2×2013=-10451.6,
∴回归直线的方程为y=5.2x-10451.6,
∴y与x是正相关关系.
(3)当x=2018时,y=5.2×2018-10451.6=42.
∴该村2018年在春节期间外出游泳的家庭数约为42.
点评 本题考查了古典概型的概率计算,线性回归方程的解法及数值估计,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 200 | 150 | 50 |
| 抽取人数 | 6 |
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
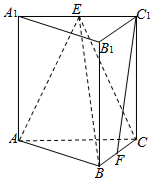 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.