题目内容
15.设函数f(x)=|2x-1|+|2x-3|,x∈R.(1)若函数f(x)=|2x-1|+|2x-3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)=$\frac{1}{f(x)+m}$的定义域为R,求实数m的取值范围.
分析 (1)根据绝对值不等式的解法,进行求解即可.
(2)将g(x)=$\frac{1}{f(x)+m}$的定义域为R,转化为(x)+m≠0在R上恒成立,即f(x)+m=0在R上无解,结合函数的最值进行求解即可.
解答 解:(1)由绝对值三角不等式可得,
f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
当且仅当$\left\{\begin{array}{l}{2x-1≥0}\\{2x-3≤0}\end{array}\right.$.即$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{x≤\frac{3}{2}}\end{array}\right.$,即x∈[$\frac{1}{2}$,$\frac{3}{2}$]]时等号成立,故f(x)的最小值为2.
(2)g(x)=$\frac{1}{f(x)+m}$的定义域为R等价于f(x)+m≠0在R上恒成立,
即f(x)+m=0在R上无解,所以m>-2,即实数m的取值范围为(-2,+∞).
点评 本题考查绝对值不等式的相关知识,考查考生的运算求解能力和等价转化能力.理解g(x)的定义域为R等价于f(x)+m≠0在R上恒成立是求解本题的关键.

练习册系列答案
相关题目
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
3.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数f(x)=x2+2ax+2有两个不同零点的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
4.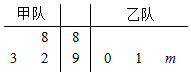 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
5.随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也在不断提高.某村村委会统计了2011到2015年五年间每年春节期间外出旅游的家庭数,具体统计数据如表所示:
(1)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\widehat y$=bx+a,
并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的直线方程估计该村2018年在春节期间外出游泳的家庭数.
参考:用最小二乘法求线性回归方程系数公式$\widehat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\widehat a=\overline y-\widehat b\overline x$.
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 18 | 22 | 26 |
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\widehat y$=bx+a,
并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的直线方程估计该村2018年在春节期间外出游泳的家庭数.
参考:用最小二乘法求线性回归方程系数公式$\widehat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\widehat a=\overline y-\widehat b\overline x$.
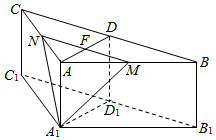 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N. 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).