题目内容
16.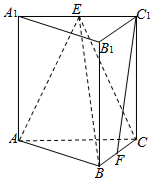 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:AB⊥C1F;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
分析 (1)由BB1⊥平面ABC得AB⊥BB1,又AB⊥BC,故AB⊥平面B1BCC1,所以AB⊥C1F;
(2)取AB的中点G,连接EG,FG.则易得四边形EGFC1是平行四边形,故而C1F∥EG,于是C1F∥平面ABE;
(3)由勾股定理求出AB,代入棱锥的体积公式计算即可.
解答 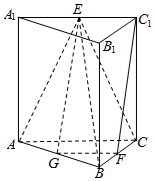 (1)证明:∵BB1⊥底面ABC,AB?平面ABC
(1)证明:∵BB1⊥底面ABC,AB?平面ABC
∴BB1⊥AB.
又∵AB⊥BC,BC?平面B1BCC1,BB1?平面B1BCC1,BC∩BB1=B,
∴AB⊥平面B1BCC1,
又∵C1F?平面B1BCC1,
∴AB⊥C1F.
(2)证明:取AB的中点G,连接EG,FG.
∵F,G分别是BC,AB的中点,
∴FG∥AC,且FG=$\frac{1}{2}$AC,
∵AC$\stackrel{∥}{=}$A1C1,E是A1C1的中点,∴EC1=$\frac{1}{2}$A1C1.
∴FG∥EC1,且FG=EC1,
∴四边形FGEC1为平行四边形,∴C1F∥EG.
又∵EG?平面ABE,C1F?平面ABE,EG?平面ABE,
∴C1F∥平面ABE.
(3)解:∵AA1=AC=2,BC=1,AB⊥BC,∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{3}$.
∴三棱锥E-ABC的体积V=$\frac{1}{3}$S△ABC•AA1=$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{3}$×1×2=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面垂直,线面平行的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
4.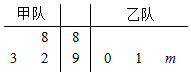 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
11.命题p:?φ∈R,函数f(x)=sin(2x+φ)不是偶函数,则¬p为( )
| A. | ?φ∈R,函数f(x)=sin(2x+φ)是奇函数 | B. | ?φ∈R,函数f(x)=sin(2x+φ)不是偶函数 | ||
| C. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 | D. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 |
8.执行如图所示的程序框图,若要使输出的y的值等于3,则输入的x的值可以是( )
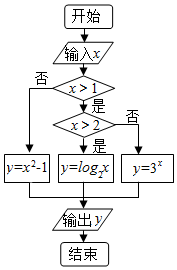

| A. | 1 | B. | 2 | C. | 8 | D. | 9 |
5.随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也在不断提高.某村村委会统计了2011到2015年五年间每年春节期间外出旅游的家庭数,具体统计数据如表所示:
(1)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\widehat y$=bx+a,
并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的直线方程估计该村2018年在春节期间外出游泳的家庭数.
参考:用最小二乘法求线性回归方程系数公式$\widehat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\widehat a=\overline y-\widehat b\overline x$.
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 18 | 22 | 26 |
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\widehat y$=bx+a,
并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的直线方程估计该村2018年在春节期间外出游泳的家庭数.
参考:用最小二乘法求线性回归方程系数公式$\widehat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\widehat a=\overline y-\widehat b\overline x$.