题目内容
已知三点M(0,-1)、A(1,-2)和B(2,1).
(1)求三角形MAB的面积.
(2)经过点M作直线l,若直线l与线段AB总有公共点,求直线l的斜率k和倾斜角α的取值范围.
(1)求三角形MAB的面积.
(2)经过点M作直线l,若直线l与线段AB总有公共点,求直线l的斜率k和倾斜角α的取值范围.
考点:三角形的面积公式,直线的倾斜角
专题:直线与圆
分析:(1)判断三角形的形状,然后求出距离,即可求三角形MAB的面积.
(2)直接求出经过点MA,MB的斜率,即可求直线l的斜率k和倾斜角α的取值范围.
(2)直接求出经过点MA,MB的斜率,即可求直线l的斜率k和倾斜角α的取值范围.
解答:
解:(1)三点M(0,-1)、A(1,-2)和B(2,1).由题意可知直线MA的斜率为:-1,直线MB的斜率为:1
可得MA⊥MB,MA=
=
,MB=
=2
,S△MAB=
×
×2
=2.
(2)由题意可知直线MA的斜率为:-1,直线MB的斜率为:1.直线l的斜率k∈[-1,1],
倾斜角的范围是:[0°,45°]∪[135°,180°)
可得MA⊥MB,MA=
| 1+(-2+1)2 |
| 2 |
| 22+(1+1)2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
(2)由题意可知直线MA的斜率为:-1,直线MB的斜率为:1.直线l的斜率k∈[-1,1],
倾斜角的范围是:[0°,45°]∪[135°,180°)
点评:本题考查三角形的面积的求法,直线的斜率以及直线的倾斜角的求法,考查计算能力.

练习册系列答案
相关题目
下列四个函数中,是奇函数的是( )
| A、f(x)=3x2 | ||
B、f(x)=
| ||
| C、f(x)=log2x | ||
| D、f(x)=x3 |
在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(x-y,x+y),则与B中元素(1,3)对应的A中的元素为( )
| A、(2,1) |
| B、(-4,3) |
| C、(-4,0) |
| D、(3,-4) |
设集合A={1,3,5},B={3,9},C={1,2},则(A∩B)∪C=( )
| A、{2} |
| B、{1,2} |
| C、{1,2,3} |
| D、{1,2,3,5,9} |
已知全集U={0,1,2,3,4},M={0,1,2},N={2,3},则(∁UM)∩N=( )
| A、{2} |
| B、{2,3,4} |
| C、{3} |
| D、{0,1,2,3,4} |
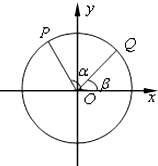 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为