题目内容
比较下列各题中值的大小:
(1)0.8-0.1,0.8-0.2
(2)1.70.3,0.93.1
(3)a1.3,a2.5
(4)P=log45,Q=log32,T=log20.3.
(1)0.8-0.1,0.8-0.2
(2)1.70.3,0.93.1
(3)a1.3,a2.5
(4)P=log45,Q=log32,T=log20.3.
考点:对数值大小的比较,不等式比较大小
专题:函数的性质及应用
分析:(1)考察指数函数y=0.8x在R上的单调递减,即可得出;
(2)由于1.70.3>1,0.93.1<1,即可得出;
(3)对a分类讨论,利用指数函数的单调性即可得出;
(4)由于P=log45>1,0<Q=log32<1,T=log20.3<0.即可得出.
(2)由于1.70.3>1,0.93.1<1,即可得出;
(3)对a分类讨论,利用指数函数的单调性即可得出;
(4)由于P=log45>1,0<Q=log32<1,T=log20.3<0.即可得出.
解答:
解:(1)考察指数函数y=0.8x在R上的单调递减,可得0.8-0.1>0.8-0.2;
(2)∵1.70.3>1,0.93.1<1,∴1.70.3>0.93.1;
(3)当0<a<1时,a1.3>a2.5;当a>1时,a1.3<a2.5;(
(4)∵P=log45>1,0<Q=log32<1,T=log20.3<0.
∴P>Q>T.
(2)∵1.70.3>1,0.93.1<1,∴1.70.3>0.93.1;
(3)当0<a<1时,a1.3>a2.5;当a>1时,a1.3<a2.5;(
(4)∵P=log45>1,0<Q=log32<1,T=log20.3<0.
∴P>Q>T.
点评:本题考查了指数函数与对数函数的单调性,属于基础题.

练习册系列答案
相关题目
函数y=log2x,x∈(0,16)的值域是( )
| A、(-∞,-4) |
| B、(-∞,4] |
| C、[-4,+∞) |
| D、[4,+∞) |
设全集U=R,A={x|x>0},B={x|x>1},则A∩∁UB=( )
| A、{x|0≤x<1} |
| B、{x|0<x≤1} |
| C、{x|x<0} |
| D、{|x>1} |
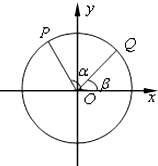 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为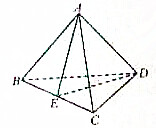 在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.
在所有棱长均为2的四面体ABCD中,E是BC的中点,写出四面体中与平面AED垂直的面,并说明理由.