题目内容
巳知集合A={x|x2＜1}，B=[0，1]，则A∩B=（ ）
| A、（0，1） |
| B、〔0，1] |
| C、[0，1） |
| D、[0，1] |
考点：交集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，找出A与B的交集即可．
解答：
解：由A中的不等式变形得：（x+1）（x-1）＜0得：-1＜x＜1，
∴A=（-1，1），
∵B=[0，1]，
∴A∩B=[0，1）．
故选：C．
∴A=（-1，1），
∵B=[0，1]，
∴A∩B=[0，1）．
故选：C．
点评：此题考查了交集及其运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
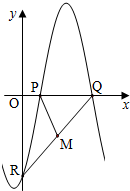如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤| π |
| 2 |
| π |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
| C、8 | ||||
| D、16 |
利用计算机产生0～1之间的均匀随机数a，则事件“
x2dx＞
”发生的概率为（ ）
| ∫ | a 0 |
| 1 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
不等式
＞x的解集是（ ）
| 1 |
| x |
| A、（-∞，-1）∪（0，1） |
| B、（-1，0）∪（0，1） |
| C、（-1，1） |
| D、（-∞，-1）∪（1，+∞） |
直线x-y+1=0的倾斜角为（ ）
| A、120° | B、60° |
| C、45° | D、30° |
已知集合A={1，2，3}，集合B={2，3，4，5}，则（ ）
| A、A⊆B |
| B、B?A |
| C、A∩B={2，3} |
| D、A∪B={1，4，5} |