Question

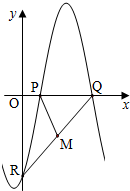如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤

π

2

）与坐标轴的三个交点P、Q、R满足P（2，0），∠PQR=

π

4

，M为QR的中点，PM=2

5

，则A的值为（　　）

• A、

  8

  3

  3

• B、

  16

  3

  3

• C、8
• D、16

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由题意设出Q（2a，0）a＞0，求出R坐标以及M坐标，利用距离公式求出Q坐标，通过五点法求出函数的解析式，即可求出A．

解答： 解：∵函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤

π

2

）与坐标轴的三个交点P、Q、R满足P（2，0），∠PQR=

π

4

，M为QR的中点，
∴设Q（2a，0），a＞0，则R（0，-2a），∴M（a，-a），
∵PM=2

5

，
∴

(a-2)2+(-a)2

=2

5

，解得a=4，
∴Q（8，0），又P（2，0），
∴

1

2

T=8-2=6，
∴T=

2π

ω

=12，解得ω=

π

6

．
∵函数经过P（2，0），R（0，-8），
∴

Asin( π 6 ×2+φ)=0 Asin( π 6 ×0+φ)=-8

，
∵|φ|≤

π

2

，
∴φ=-

π

3

，
解得A=

16

3

3

，
故选：B．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得Q点与P点的坐标是关键，考查识图、运算与求解能力，属于中档题．