题目内容
17.函数y=f(x)导函数的图象如图所示,则下列说法错误的是( )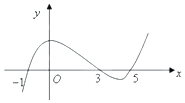
| A. | (-1,3)为函数y=f(x)的递增区间 | B. | (3,5)为函数y=f(x)的递减区间 | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
分析 利用导数与函数单调性的关系以及函数在某点取得极值的条件即可判断.
解答 解:由函数y=f(x)导函数的图象可知:
当x<-1及3<x<5时,f′(x)<0,f(x)单调递减;
当-1<x<3及x>5时,f′(x)>0,f(x)单调递增.
所以f(x)的单调减区间为(-∞,-1),(3,5);
单调增区间为(-1,3),(5,+∞),
f(x)在x=-1,5取得极小值,在x=3处取得极大值,
故选项C错误;
故选:C.
点评 本题考查函数的单调性及极值问题,本题以图象形式给出导函数,由此研究函数有关性质,体现了数形结合思想.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
7.已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若x2<f(x1)<x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数可能为( )
| A. | 3,4,5 | B. | 4,5,6 | C. | 2,4,5 | D. | 2,3,4 |
8.某公司的班车分别在7:30,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过15分钟的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{8}$ |
2.某公司安排6位员工在“元旦(1月1日至1月3日)”假期值班,每天安排2人,每人值班1天,则6位员工中甲不在1日值班的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |