题目内容
3.在平面直角坐标系中,△ABC三个顶点分别为A(2,4),B(1,-3),C(-2,1).(1)求BC边上的高所在的直线方程;
(2)设AC中点为D,求△DBC的面积.
分析 (1)kBC=-$\frac{4}{3}$,可得BC边上的高所在的直线的斜率为$\frac{3}{4}$.利用点斜式可得BC边上的高所在的直线方程.
(2)BC边所在的直线方程为:y+3=-$\frac{4}{3}$(x-1),化为:4x+3y+5=0.可得AC的中点D$(0,\frac{5}{2})$.利用点D到直线BC的距离d.又|BC|,可得S△DBC=$\frac{1}{2}|BC|•d$.
解答 解:(1)kBC=$\frac{-3-1}{1+2}$=-$\frac{4}{3}$,∴BC边上的高所在的直线的斜率为$\frac{3}{4}$.
则BC边上的高所在的直线方程为:y-4=$\frac{3}{4}$(x-2),化为:3x-4y+10=0.
(2)BC边所在的直线方程为:y+3=-$\frac{4}{3}$(x-1),化为:4x+3y+5=0.
∵D是AC的中点,∴D$(0,\frac{5}{2})$.
点D到直线BC的距离d=$\frac{|4×0+3×\frac{5}{2}+5|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{5}{2}$.
又|BC|=$\sqrt{(-2-1)^{2}+(1+3)^{2}}$=5,
∴S△DBC=$\frac{1}{2}|BC|•d$=$\frac{1}{2}×5×\frac{5}{2}$=$\frac{25}{4}$.
点评 本题考查了直线的方程、中点坐标公式、相互垂直的直线斜率之间的关系、点到直线的距离公式、两点之间的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
2.某公司安排6位员工在“元旦(1月1日至1月3日)”假期值班,每天安排2人,每人值班1天,则6位员工中甲不在1日值班的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
14.已知双曲线C与双曲线$\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{48}$=1有相同的渐近线,且与椭圆$\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{169}$=1有相同的焦点,则双曲线C的方程为( )
| A. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
11.已知倾斜角60°为的直线l平分圆:x2+y2+2x+4y-4=0,则直线l的方程为( )
| A. | $\sqrt{3}$x-y+$\sqrt{3}$+2=0 | B. | $\sqrt{3}$x+y+$\sqrt{3}$+2=0 | C. | $\sqrt{3}$x-y+$\sqrt{3}$-2=0 | D. | $\sqrt{3}$x-y-$\sqrt{3}$+2=0 |
18.已知点P(t,t-1),t∈R,点E是圆x2+y2=$\frac{1}{4}$上的动点,点F是圆(x-3)2+(y+1)2=$\frac{9}{4}$上的动点,则|PF|-|PE|的最大值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
13.在如图所示的程序框图中,若输入的m=98,n=63,则输出的结果为( )
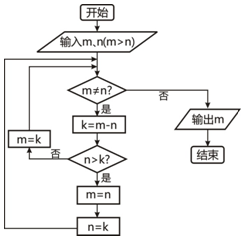

| A. | 9 | B. | 8 | C. | 7 | D. | 6 |