题目内容
20.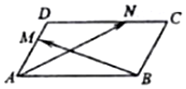 如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )
如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )| A. | [-3,1] | B. | [-3,-1] | C. | [-1,1] | D. | [1,3] |
分析 画出图形,建立直角坐标系,求出B,A,D的坐标,利用比例关系和向量的运算求出$\overrightarrow{AN}$,$\overrightarrow{BM}$的坐标,然后通过二次函数的单调性,求出数量积的范围.
解答 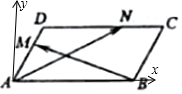 解:建立如图所示的以A为原点,
解:建立如图所示的以A为原点,
AB,AD所在直线为x,y轴的直角坐标系,
则B(2,0),A(0,0),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
∵满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,λ∈[0,1],
$\overrightarrow{AN}$=$\overrightarrow{AD}$+$\overrightarrow{DN}$=$\overrightarrow{AD}$+(1-λ)$\overrightarrow{DC}$=$\overrightarrow{AD}$+(1-λ)$\overrightarrow{AB}$
=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)+(1-λ)(2,0)
=($\frac{5}{2}$-2λ,$\frac{\sqrt{3}}{2}$);
$\overrightarrow{BM}$=$\overrightarrow{BA}$+$\overrightarrow{AM}$=-$\overline{\;}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AD}$
=(-2,0)+(1-λ)($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=(-$\frac{3}{2}$-$\frac{1}{2}$λ,$\frac{\sqrt{3}}{2}$(1-λ)),
则$\overrightarrow{AN}$•$\overrightarrow{BM}$=($\frac{5}{2}$-2λ,$\frac{\sqrt{3}}{2}$)•(-$\frac{3}{2}$-$\frac{1}{2}$λ,$\frac{\sqrt{3}}{2}$(1-λ))
=($\frac{5}{2}$-2λ)(-$\frac{3}{2}$-$\frac{1}{2}$λ)+$\frac{\sqrt{3}}{2}$•$\frac{\sqrt{3}}{2}$(1-λ)
=λ2+λ-3=(λ+$\frac{1}{2}$)2-$\frac{13}{4}$,
因为λ∈[0,1],二次函数的对称轴为:λ=-$\frac{1}{2}$,
则[0,1]为增区间,
故当λ∈[0,1]时,λ2+λ-3∈[-3,-1].
故选:B.
点评 本题考查向量的综合应用,平面向量的坐标表示以及数量积的应用,二次函数的最值问题,考查计算能力,属于中档题.

| A. | -2或1 | B. | 0或1 | C. | -2或-1 | D. | 0或-2 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
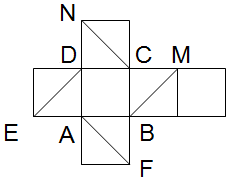 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).