题目内容
8.已知数列{an}中,a1=1,an+1=1+$\frac{2}{{a}_{n}}$,记bn=$\frac{{a}_{n}-2}{{a}_{n}+1}$(1)求证:数列{bn}是等比数列,并求bn;
(2)求数列{an}的通项公式an;
(3)记cn=nbn,Sn=c1+c2+…+cn,对任意正整数n,不等式$\frac{m}{32}$+$\frac{3}{2}$Sn+n(-$\frac{1}{2}$)n+1-$\frac{1}{3}$(-$\frac{1}{2}$)n>0恒成立,求最小正整数m.
分析 (1)bn=$\frac{{a}_{n}-2}{{a}_{n}+1}$,an+1=1+$\frac{2}{{a}_{n}}$,可得bn+1=$\frac{{a}_{n+1}-2}{{a}_{n+1}+1}$=$\frac{1+\frac{2}{{a}_{n}}-2}{1+\frac{2}{{a}_{n}}+1}$=-$\frac{1}{2}$$\frac{{a}_{n}-2}{{a}_{n}+1}$=-$\frac{1}{2}{b}_{n}$.即可证明.
(2)由bn=$\frac{{a}_{n}-2}{{a}_{n}+1}$=$(-\frac{1}{2})^{n}$,解出即可得出an.
(3)cn=nbn=n$(-\frac{1}{2})^{n}$,利用“错位相减法”与不等式的性质即可得出.
解答 (1)证明:∵bn=$\frac{{a}_{n}-2}{{a}_{n}+1}$,an+1=1+$\frac{2}{{a}_{n}}$,
∴bn+1=$\frac{{a}_{n+1}-2}{{a}_{n+1}+1}$=$\frac{1+\frac{2}{{a}_{n}}-2}{1+\frac{2}{{a}_{n}}+1}$=-$\frac{1}{2}$$\frac{{a}_{n}-2}{{a}_{n}+1}$=-$\frac{1}{2}{b}_{n}$.
∴数列{bn}是等比数列,公比为-$\frac{1}{2}$,且首项为-$\frac{1}{2}$.
∴bn=$(-\frac{1}{2})^{n}$.
(2)由bn=$\frac{{a}_{n}-2}{{a}_{n}+1}$=$(-\frac{1}{2})^{n}$,得an=$\frac{{2}^{n+1}+(-1)^{n}}{{2}^{n}+(-1)^{n-1}}$.
(3)cn=nbn=n$(-\frac{1}{2})^{n}$,
∴Sn=-$\frac{1}{2}$+2×$(-\frac{1}{2})^{2}$+3×$(-\frac{1}{2})^{3}$+…+n$•(-\frac{1}{2})^{n}$,
$-\frac{1}{2}{S}_{n}$=$(-\frac{1}{2})^{2}+2(-\frac{1}{2})^{3}$+…+$(n-1)×(-\frac{1}{2})^{n}$+n$•(-\frac{1}{2})^{n+1}$,
两式相减得$\frac{3}{2}$Sn=-$\frac{1}{3}$$[1-(-\frac{1}{2})^{n}]$-n$(-\frac{1}{2})^{n+1}$,
∴不等式$\frac{m}{32}$+$\frac{3}{2}$Sn+n(-$\frac{1}{2}$)n+1-$\frac{1}{3}$(-$\frac{1}{2}$)n>0,
即$\frac{m}{32}-\frac{1}{3}$>0,解得m$>\frac{32}{3}$,因此m≥11.
因此最小的正整数m=11.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、“错位相减法”,考查了推理能力与计算能力,属于难题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 2 | B. | 3 | ||
| C. | 4 | D. | 与点位置有关的值 |
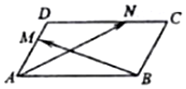 如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )
如图,在平行四边形ABCD中,∠BAD=$\frac{π}{3}$,AB=2,AD=1,若M、N分别是边AD、CD上的点,且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ,其中λ∈[0,1],则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是( )| A. | [-3,1] | B. | [-3,-1] | C. | [-1,1] | D. | [1,3] |
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
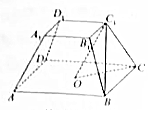 如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4.
如图,正四棱台ABCD-A1B1C1D1的高为2,下底面中心为O,上、下底面边长分别为2和4. 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.